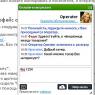
Nâng ma trận lên lũy thừa. Một số tính chất của phép toán trên ma trận.

Phép toán nâng lũy thừa n có thể được áp dụng chính thức cho ma trận vuông. Để làm điều này, n phải là số nguyên. Kết quả của hoạt động này được đưa ra trong bảng. 9.1. Bạn có thể nhập toán tử để nâng ma trận m lên lũy thừa n theo cách tương tự như đối với đại lượng vô hướng: bằng cách nhấp vào nút Tăng lên Nguồn trên bảng Máy tính hoặc bằng cách nhấn phím<А>. Sau khi placeholder xuất hiện, bạn nhập giá trị độ n vào đó.

Bảng 9.1. Kết quả nâng ma trận lên lũy thừa

0 ma trận đồng nhất của chiều ma trận M

1 chính ma trận M

1 M -1 - ma trận nghịch đảo của M

2,3,...MM, (MM)M, ...

2, -3, ... M -1 M -1 , (M -1 M -1)M -1 , ...

Một số ví dụ về việc nâng ma trận lên lũy thừa được trình bày trong Liệt kê 9.15.

Liệt kê 9.15. Ví dụ về nâng ma trận vuông lên lũy thừa số nguyên

Vector hóa mảng

Đại số vectơ của Mathcad bao gồm một toán tử hơi khác thường được gọi là toán tử vectorize. Toán tử này thường được dùng để làm việc với mảng. Nó cho phép bạn thực hiện cùng một loại thao tác trên tất cả các phần tử của một mảng (tức là ma trận hoặc vectơ), do đó đơn giản hóa việc lập trình các vòng lặp. Ví dụ: đôi khi bạn muốn nhân mỗi phần tử của một vectơ với phần tử tương ứng của vectơ khác. Không có thao tác nào như vậy trực tiếp trong Mathcad, nhưng nó có thể được thực hiện dễ dàng bằng cách sử dụng vector hóa (Liệt kê 9.16). Đối với điều này:

· Nhập biểu thức vectơ như ở dòng thứ hai của danh sách (lưu ý rằng ở dạng này ký hiệu nhân biểu thị toán tử tích vô hướng của vectơ).

· Di chuyển con trỏ sao cho các dòng đầu vào làm nổi bật toàn bộ biểu thức cần được vector hóa (Hình 9.3).

Nhập toán tử vector hóa bằng cách nhấp vào nút Vectorize trên bảng Ma trận (Hình 9.3) hoặc sử dụng phím tắt +<->.

· Đi vào<=>để có được kết quả.

Cơm. 9.3. Toán tử vector hóa

Liệt kê 9.16. Sử dụng vectorization để nhân các phần tử của một vector

Toán tử vector hóa chỉ có thể được sử dụng với các vectơ và ma trận có cùng kích thước.

Hầu hết các hàm Mathcad không cụ thể không yêu cầu vector hóa để thực hiện cùng một thao tác trên tất cả các phần tử của vectơ. Ví dụ, lập luận hàm lượng giác theo định nghĩa là một đại lượng vô hướng. Nếu bạn cố tính sin của một đại lượng vectơ, Mathcad sẽ vectơ hóa theo mặc định, tính sin của từng phần tử và tạo ra vectơ tương ứng làm kết quả. Một ví dụ được hiển thị trong Liệt kê 9.17.

Liệt kê 9.17. Vector hóa là tùy chọn cho hầu hết các hàm Mathcad

Các phép toán tượng trưng với ma trận

Tất cả các toán tử ma trận và vectơ được thảo luận ở trên có thể được sử dụng trong tính toán tượng trưng. Sức mạnh của các phép toán biểu tượng nằm ở khả năng thực hiện chúng không chỉ trên các con số cụ thể mà còn trên các biến. Một số ví dụ được hiển thị trong Liệt kê 9.18.

Liệt kê 9.18. Ví dụ về các phép toán ký hiệu trên vectơ và ma trận

Hãy thoải mái sử dụng bộ xử lý ký hiệu như một tài liệu tham khảo toán học hữu ích. Ví dụ, khi bạn muốn nhớ lại một số định nghĩa từ trường đại số tuyến tính (ví dụ: các quy tắc nhân và nghịch đảo ma trận được hiển thị trong các dòng đầu tiên của Liệt kê 9.18).

Hàm ma trận

Hãy liệt kê các hàm dựng sẵn chính được thiết kế để giúp làm việc với vectơ và ma trận dễ dàng hơn. Chúng cần thiết để tạo ma trận, hợp nhất và chọn các phần của ma trận, thu được các tính chất cơ bản của ma trận, v.v.

Hàm tạo ma trận

Cách trực quan nhất để tạo ma trận hoặc vectơ là sử dụng nút đầu tiên trên thanh công cụ Ma trận. Tuy nhiên, trong hầu hết các trường hợp, đặc biệt là khi lập trình các dự án phức tạp, sẽ thuận tiện hơn khi tạo mảng bằng các hàm dựng sẵn.

Xác định các phần tử ma trận bằng hàm

· ma trận(M,N,f) - tạo một ma trận có kích thước M*N, mỗi phần tử i, j của nó là f(i, j) (Liệt kê 9.19);

o M - số dòng;

o N - số cột;

o f(i,j) – hàm.

Liệt kê 9.19. Tạo ma trận

Để tạo ma trận, có hai hàm cụ thể hơn, được sử dụng chủ yếu để trình bày nhanh chóng và hiệu quả mọi phụ thuộc dưới dạng biểu đồ ba chiều (chẳng hạn như bề mặt hoặc đường cong không gian). Tất cả các đối số của chúng, ngoại trừ đối số đầu tiên (hàm), đều là tùy chọn. Hãy xem xét chức năng đầu tiên.

CreateSpace(F(or f1, f2, f3), t0, t1, tgrid, fmap) - tạo một mảng lồng nhau biểu thị tọa độ x-, y- và z của đường cong không gian tham số, hàm đã cho R;

F(t) là hàm vectơ gồm ba phần tử, được xác định theo tham số đối với một đối số t;
f1(t),f2(t), f3(t) - hàm vô hướng;
t0 - giới hạn dưới t (mặc định -5);
t1 - giới hạn trên t (mặc định 5);
tgrid - số điểm lưới theo biến t (mặc định 2o);
fmap là một hàm vectơ gồm ba đối số xác định phép biến đổi tọa độ.

Cơm. 9.4. Sử dụng hàm CreateSpace với một bộ tham số khác

Một ví dụ về việc sử dụng hàm CreateSpace được hiển thị trong Hình 2. 9.4. Lưu ý rằng không cần tốn nhiều công sức để vẽ đồ thị xoắn ốc. mã bổ sung, ngoại trừ việc xác định sự phụ thuộc tham số trong hàm vectơ F.

Hàm tạo ma trận cho biểu đồ bề mặt 3D được thiết kế theo cách giống hệt nhau, ngoại trừ việc định nghĩa bề mặt yêu cầu hai biến thay vì một. Một ví dụ về việc sử dụng nó được minh họa trong hình. 9,5.

Cơm. 9,5. Sử dụng hàm CreateMesh với một bộ tham số khác

· CreateMesh(F(or g, or f1, f2, f3) , s0, s1, t0, t1, sgrid, tgrid, fmap) - tạo một mảng lồng nhau biểu thị tọa độ x-, y- và z của bề mặt tham số được chỉ định bởi hàm F;

F(s,t) là hàm vectơ gồm ba phần tử, được xác định bằng tham số đối với hai đối số s và t;
g(s,t) - hàm vô hướng;
f1(s,t),f2(s,t),f3(s,t) - hàm vô hướng;
s0, t0 - giới hạn dưới của đối số s, t (mặc định -5);
s1, t1 - giới hạn trên của đối số s, t (mặc định 5);
sgrid, tgrid - số điểm lưới dựa trên biến s và t (mặc định 20);
fmap là một hàm vectơ ba phần tử gồm ba đối số xác định phép biến đổi tọa độ.

Ví dụ về các mảng lồng nhau được tạo bởi các hàm CreateMesh và CreateSpace được hiển thị trong Liệt kê 9.20. Mỗi ma trận của ba ma trận lồng nhau tạo thành mảng xác định tọa độ x-, y- và z của các điểm trên bề mặt hoặc đường cong tương ứng.

Liệt kê 9.20. Kết quả của hàm CreateMesh và CreateSpace (Hình 9.4 - 9.5)

Tạo ma trận loại đặc biệt

Tạo ma trận trong Mathcad dễ dàng loại nhất định bằng cách sử dụng một trong các chức năng tích hợp sẵn. Ví dụ về việc sử dụng các hàm này được hiển thị trong Liệt kê 9.21.

· nhận dạng (N) - ma trận nhận dạng có kích thước N*N;

· diag(v) - ma trận đường chéo, trên đường chéo của nó là các phần tử của vectơ v;

· geninv(A) - tạo ma trận nghịch đảo (ở bên trái) của ma trận A;

· rref (A) - chuyển đổi ma trận hoặc vectơ A sang dạng từng bước;

N - số nguyên;
v - vectơ;
A là ma trận các số thực.

Kích thước N*M của ma trận A cho hàm geninv phải sao cho N>M.

Liệt kê 9.21. Tạo ma trận thuộc loại đặc biệt

GHI CHÚ

Trong Mathcad 14 và 15, việc vector hóa có thể được thực hiện không chỉ bằng số mà còn bằng các phép tính tượng trưng (phân tích).

Hầu hết các hàm Mathcad không cụ thể không yêu cầu vector hóa để thực hiện cùng một thao tác trên tất cả các phần tử của vectơ. Ví dụ, đối số của hàm lượng giác, theo định nghĩa, là một đại lượng vô hướng. Nếu bạn cố gắng tính số mũ của một đại lượng vectơ, Mathcad sẽ vector hóa theo mặc định, nâng từng phần tử lên lũy thừa e và tạo ra vectơ tương ứng như kết quả (Liệt kê 7.13).

Liệt kê 7.13. Vector hóa đối số là tùy chọn cho hầu hết các hàm tích hợp trong Mathcad

7.3. Tính định thức và nghịch đảo ma trận vuông

Chúng ta hãy xem xét một số phép tính cực kỳ quan trọng khác của đại số tuyến tính liên quan đến khái niệm định thức của ma trận. Mặc dù thực tế là một số trong số chúng cũng được triển khai trong Mathcad dưới dạng toán tử, nhưng chúng yêu cầu (khi thực hiện các phép tính bằng thuật toán số) nhiều sự chú ý hơn so với các toán tử được đề cập trong hai phần trước.

7.3.1. Định thức của ma trận vuông

Định thức của ma trận được ký hiệu bằng chuẩn ký hiệu toán học. Để nhập toán tử tìm định thức của ma trận, bạn có thể nhấp vào nút Xác định trên thanh công cụ Ma trận (Liệt kê 7.14) hoặc gõ trên bàn phím<|>(bằng cách nhấn phím +<\>). Kết quả của bất kỳ hành động nào trong số này là một phần giữ chỗ sẽ xuất hiện để đặt ma trận vào đó. Để tính định thức của ma trận đã được nhập:

1. Di chuyển con trỏ trong tài liệu để đặt ma trận giữa các dòng đầu vào (hãy nhớ rằng các dòng đầu vào là các đoạn dọc và ngang có màu xanh, tạo thành một góc trỏ đến vùng chỉnh sửa hiện tại).

2. Nhập toán tử tìm định thức của ma trận.

3. Nhập dấu bằng (hoặc đầu ra tượng trưng) để tính định thức (tương ứng bằng số hoặc giải tích, như trong Liệt kê

CHÚ Ý!

Đừng nhầm lẫn giữa các toán tử tính định thức của ma trận vuông và độ dài của vectơ. Bắt đầu với Mathcad 12, việc kiểm soát bắt buộc các hành động của người dùng khi nhập các toán tử này đã được giới thiệu để tránh nhầm lẫn (vì các ký hiệu này được sử dụng giống nhau cho các toán tử này).

hai thao tác). Nếu bạn cố tính định thức của ma trận bằng toán tử A được nhập từ bảng Máy tính thay vì bảng Ma trận, một thông báo lỗi sẽ hiển thị và kết quả của phép tính định thức sẽ chỉ xuất hiện sau khi người dùng gọi danh mục và sẽ xác nhận trong đó rằng anh ta sẽ tính chính xác định thức của ma trận. Điều tương tự cũng áp dụng cho độ dài vectơ nếu bạn cố gắng nhập nó không phải từ bảng Máy tính mà từ bảng Ma trận.

Liệt kê 7.14. Tính định thức của ma trận vuông

7.3.2. Xếp hạng ma trận

Thứ hạng của ma trận là số tự nhiên k lớn nhất mà có định thức khác 0 của cấp thứ k của ma trận con bao gồm bất kỳ giao điểm nào của k cột và k hàng của ma trận.

Để tính thứ hạng trong Mathcad, hãy sử dụng hàm xếp hạng (Liệt kê 7.15).

 hạng(A) - hạng ma trận: A - ma trận.

Liệt kê 7.15. Tính thứ hạng ma trận

7.3.3. Đảo ngược ma trận vuông

Tìm kiếm ma trận nghịch đảo có thể nếu ma trận vuông và định thức của nó không bằng 0. Theo định nghĩa, tích của ma trận ban đầu và ma trận nghịch đảo của nó là ma trận đơn vị. Để nhập toán tử tìm kiếm ma trận nghịch đảo, nhấp vào nút Nghịch đảo trên thanh công cụ Ma trận. Liệt kê 7.16 cho thấy một ví dụ về việc tìm nghịch đảo của một ma trận và sau đó xác minh rằng nó đã được tính toán chính xác.

Liệt kê 7.16. Tính ma trận nghịch đảo

7.3.4. Nâng ma trận vuông lên lũy thừa

Phép tính lũy thừa n có thể được áp dụng chính thức cho ma trận vuông. Để làm điều này, n phải là số nguyên. Kết quả của hoạt động này được đưa ra trong bảng. 7.1. Bạn có thể nhập toán tử để nâng ma trận M lên lũy thừa n theo cách tương tự như đối với đại lượng vô hướng: bằng cách nhấn nút lũy thừa(Tăng lên nguồn) trong bảng Máy tính hoặc bằng cách nhấn phím<^>. Sau khi placeholder xuất hiện, bạn nhập giá trị độ n vào đó.

	Bảng 7.1. Quy tắc nâng ma trận lên lũy thừa



	Ma trận đồng nhất của chiều ma trận M

	Bản thân ma trận M

	M -1 - ma trận, nghịch đảo M

	Đại số tuyến tính
		Bảng 7.1 (cuối)


	2 ,3 , ...	M M, (M M) M, ...

	–2 , –3 , ...	M-1 M-1 , (M-1 M-1 ) M-1 , ...

Các ví dụ về việc nâng ma trận lên lũy thừa được đưa ra trong Liệt kê 7.17.

Liệt kê 7.17. Nâng ma trận vuông lên lũy thừa số nguyên

7.3.5. Định mức ma trận

Trong đại số tuyến tính, nhiều vectơ và định mức ma trận (chuẩn) khác nhau được sử dụng để gán một đặc tính số vô hướng nhất định cho ma trận. Chuẩn ma trận phản ánh thứ tự độ lớn của các phần tử ma trận. Trong các bài toán cụ thể khác nhau của đại số tuyến tính, chúng được sử dụng các loại khác nhau Bình thường Mathcad có bốn hàm dựng sẵn để tính các định mức khác nhau của ma trận vuông:

norm1(A) - chuẩn trong không gian L1;

norm2(A) - chuẩn trong không gian L2;

Một số tính chất của phép toán trên ma trận.
Biểu thức ma trận

Và bây giờ sẽ là phần tiếp theo của chủ đề, trong đó chúng ta sẽ xem xét không chỉ tài liệu mới mà còn cả cách giải quyết các phép toán với ma trận.

Một số tính chất của phép toán trên ma trận

Có khá nhiều tính chất liên quan đến các phép toán với ma trận, trong cùng một Wikipedia, bạn có thể chiêm ngưỡng thứ hạng có trật tự của các quy tắc tương ứng. Tuy nhiên, trong thực tế, nhiều tính chất theo một nghĩa nào đó là “chết”, vì chỉ một số ít trong số chúng được sử dụng để giải các bài toán thực tế. Mục tiêu của tôi là xem xét ứng dụng thực tế của các tính chất trên ví dụ cụ thể, và nếu bạn cần một lý thuyết chặt chẽ, vui lòng sử dụng nguồn thông tin khác.

Chúng ta hãy nhìn vào một số ngoại lệ cho quy tắc, sẽ được yêu cầu để hoàn thành các nhiệm vụ thực tế.

Nếu ma trận vuông có ma trận nghịch đảo, thì phép nhân của chúng có tính chất giao hoán:

Ma trận đơn vịđược gọi là ma trận vuông có đường chéo chính các đơn vị được định vị và các phần tử còn lại bằng 0. Ví dụ: , v.v.

trong đó tính chất sau đây là đúng: nếu nhân một ma trận tùy ý trái hay phải vào ma trận nhận dạng kích thước phù hợp, thì kết quả là ma trận ban đầu:

Như bạn có thể thấy, tính giao hoán của phép nhân ma trận cũng diễn ra ở đây.

Hãy lấy một số ma trận, giả sử, ma trận từ bài toán trước: .

Những người quan tâm có thể kiểm tra và đảm bảo rằng:

Ma trận đơn vị của ma trận là một ma trận tương tự của đơn vị số cho các số, điều này đặc biệt rõ ràng từ các ví dụ vừa được thảo luận.

Tính giao hoán của một hệ số đối với phép nhân ma trận

Đối với ma trận và số thực tính chất sau giữ:

Nghĩa là, hệ số số có thể (và nên) được di chuyển về phía trước để nó “không cản trở” việc nhân ma trận.

Ghi chú : nói chung, việc xây dựng thuộc tính chưa đầy đủ - “lambda” có thể được đặt ở bất kỳ đâu giữa các ma trận, thậm chí ở cuối. Quy tắc vẫn hợp lệ nếu nhân ba ma trận trở lên.

Ví dụ 4

Tính toán sản phẩm

Giải pháp:

(1) Theo tài sản di chuyển hệ số về phía trước. Bản thân các ma trận không thể được sắp xếp lại!

(2) – (3) Thực hiện phép nhân ma trận.

(4) Ở đây bạn có thể chia mỗi số cho 10, nhưng sau đó sẽ xuất hiện giữa các phần tử của ma trận số thập phân, điều đó không tốt. Tuy nhiên, chúng tôi nhận thấy rằng tất cả các số trong ma trận đều chia hết cho 5 nên chúng tôi nhân từng phần tử với .

Trả lời:

Một trò chơi đố chữ nhỏ dành cho quyết định độc lập:

Ví dụ 5

Tính toán nếu

Đáp án và đáp án ở cuối bài.

Kỹ thuật nào là quan trọng khi giải các ví dụ như vậy? Chúng ta hãy tìm ra những con số cuối cùng .

Hãy gắn một cỗ xe khác vào đầu máy:

Làm thế nào để nhân ba ma trận?

Trước hết, kết quả sẽ là gì nhân ba ma trận? Mèo sẽ không sinh ra chuột. Nếu phép nhân ma trận khả thi thì kết quả cũng sẽ là ma trận. Hmmm, giáo viên đại số của tôi không hiểu cách tôi giải thích tính khép kín của cấu trúc đại số so với các phần tử của nó =)

Tích của ba ma trận có thể được tính theo hai cách:

1) tìm rồi nhân với ma trận “ce”: ;

2) trước tiên hãy tìm , sau đó nhân .

Kết quả chắc chắn sẽ trùng khớp, và trên lý thuyết tài sản này gọi là tính kết hợp của phép nhân ma trận:

Ví dụ 6

Nhân ma trận theo hai cách

Thuật toán các giải pháp hai bước: chúng ta tìm tích của hai ma trận, sau đó chúng ta lại tìm tích của hai ma trận.

1) Sử dụng công thức

Hành động một:

Màn hai:

2) Sử dụng công thức

Hành động một:

Màn hai:

Trả lời:

Tất nhiên, giải pháp đầu tiên quen thuộc và tiêu chuẩn hơn, trong đó “mọi thứ dường như đã ổn thỏa”. Nhân tiện, về thứ tự. Trong nhiệm vụ đang được xem xét, thường nảy sinh ảo tưởng rằng chúng ta đang nói về một số loại hoán vị của ma trận. Họ không có ở đây. Tôi nhắc bạn lần nữa rằng V. trường hợp chung KHÔNG THỂ ĐẢO NGƯỢC Ma trận. Vì vậy, trong đoạn thứ hai, ở bước thứ hai, chúng ta thực hiện phép nhân, nhưng không bao giờ thực hiện . Với các số thông thường, một số như vậy sẽ có tác dụng, nhưng với ma trận thì không.

Tính chất của phép nhân kết hợp không chỉ đúng với ma trận bình phương mà còn đúng với ma trận tùy ý - miễn là chúng được nhân với nhau:

Ví dụ 7

Tìm tích của ba ma trận

Đây là ví dụ để bạn tự giải quyết. Trong giải pháp mẫu, việc tính toán được thực hiện theo hai cách; phân tích con đường nào có lợi hơn và ngắn hơn.

Tính chất kết hợp của phép nhân ma trận cũng đúng cho số lượng nhiều hơn số nhân.

Bây giờ là lúc quay trở lại với lũy thừa của ma trận. Bình phương của ma trận được xem xét ngay từ đầu và câu hỏi trong chương trình nghị sự là:

Làm thế nào để lập phương một ma trận và lũy thừa cao hơn?

Các phép toán này cũng chỉ được xác định cho ma trận vuông. Để xây dựng Ma trận vuông thành khối lập phương, bạn cần tính tích:

Trên thực tế nó là trương hợp đặc biệt phép nhân ba ma trận, theo tính chất kết hợp của phép nhân ma trận: . Và ma trận nhân với chính nó là bình phương của ma trận:

Vì vậy, chúng ta có được công thức làm việc:

Nghĩa là, nhiệm vụ được thực hiện theo hai bước: đầu tiên, ma trận phải được bình phương, sau đó ma trận thu được phải được nhân với ma trận.

Ví dụ 8

Xây dựng ma trận thành một khối.

Đây là một vấn đề nhỏ bạn có thể tự giải quyết.

Việc nâng ma trận lên lũy thừa 4 được thực hiện một cách tự nhiên:

Sử dụng tính kết hợp của phép nhân ma trận, chúng ta rút ra được hai công thức làm việc. Thứ nhất: – đây là tích của ba ma trận.

1) . Nói cách khác, trước tiên chúng ta tìm , sau đó nhân nó với “be” - chúng ta nhận được một khối lập phương, và cuối cùng, chúng ta thực hiện lại phép nhân - sẽ có lũy thừa thứ tư.

2) Nhưng có một giải pháp ngắn hơn một bước: . Nghĩa là, trong bước đầu tiên, chúng ta tìm một hình vuông và bỏ qua khối lập phương, thực hiện phép nhân

Nhiệm vụ bổ sungđến ví dụ 8:

Nâng ma trận lên lũy thừa thứ tư.

Như vừa lưu ý, điều này có thể được thực hiện theo hai cách:

1) Vì khối lập phương đã biết nên chúng ta thực hiện phép nhân.

2) Tuy nhiên, nếu theo điều kiện của bài toán cần xây dựng ma trận chỉ đến sức mạnh thứ tư, thì việc rút ngắn đường đi sẽ thuận lợi hơn - tìm bình phương của ma trận và sử dụng công thức.

Cả lời giải và đáp án đều có ở cuối bài.

Tương tự, ma trận được nâng lên lũy thừa thứ năm trở lên. Từ kinh nghiệm thực tế, tôi có thể nói rằng đôi khi tôi bắt gặp những ví dụ về việc nâng cấp lũy thừa thứ 4, nhưng tôi không nhớ gì về lũy thừa thứ năm. Nhưng để đề phòng, tôi sẽ đưa ra thuật toán tối ưu:

1) tìm ;
2) tìm ;
3) nâng ma trận lên lũy thừa thứ năm: .

Có lẽ đây là tất cả các tính chất cơ bản của phép toán ma trận có thể hữu ích trong các bài toán thực tế.

Trong phần thứ hai của bài học, dự kiến sẽ có một đám đông đầy màu sắc không kém.

Biểu thức ma trận

Hãy lặp lại các cách diễn đạt thông thường ở trường với các con số. Một biểu thức số bao gồm các số, ký hiệu toán học và dấu ngoặc đơn, ví dụ: . Khi tính toán, ưu tiên đại số quen thuộc được áp dụng: đầu tiên, dấu ngoặc đơn, sau đó thực hiện lũy thừa/root, Sau đó phép nhân/chia và cuối cùng nhưng không kém phần quan trọng - phép cộng/trừ.

Nếu một biểu thức số có ý nghĩa thì kết quả đánh giá của nó là một số, Ví dụ:

Biểu thức ma trậnđược sắp xếp gần giống nhau! Với sự khác biệt là nhân vật chính là ma trận. Cộng với một số phép toán ma trận cụ thể, chẳng hạn như chuyển vị và tìm nghịch đảo của ma trận.

Hãy xem xét biểu thức ma trận , một số ma trận ở đâu. Trong biểu thức ma trận này, ba số hạng và các phép tính cộng/trừ được thực hiện cuối cùng.

Ở số hạng đầu tiên, trước tiên bạn cần hoán vị ma trận “be”: , sau đó thực hiện phép nhân và nhập “hai” vào ma trận thu được. lưu ý rằng hoạt động chuyển vị có nhiều hơn ưu tiên cao hơn phép nhân. Dấu ngoặc đơn, như trong biểu thức số, thay đổi thứ tự các hành động: – ở đây phép nhân được thực hiện trước, sau đó ma trận kết quả được hoán vị và nhân với 2.

Trong thuật ngữ thứ hai, phép nhân ma trận được thực hiện đầu tiên và ma trận nghịch đảo được tìm thấy từ tích. Nếu bỏ dấu ngoặc: thì trước tiên bạn cần tìm ma trận nghịch đảo rồi nhân các ma trận: . Việc tìm nghịch đảo của ma trận cũng được ưu tiên hơn phép nhân.

Với số hạng thứ ba, mọi thứ đều rõ ràng: chúng ta nâng ma trận thành khối lập phương và nhập số “năm” vào ma trận thu được.

Nếu một biểu thức ma trận có ý nghĩa thì kết quả đánh giá của nó là một ma trận.

Tất cả các nhiệm vụ sẽ được thực hiện từ những nhiệm vụ thực tế kiểm tra, và chúng ta sẽ bắt đầu với cách đơn giản nhất:

Ví dụ 9

ma trận đã cho . Tìm thấy: