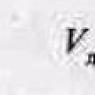Search for MS EXCEL solution. Acquaintance. Preparing an optimization model in MS EXCEL
. Simplex method algorithm
Example 5.1. Solve the following problem linear programming simplex method:
Solution:
I iteration:

x3, x4, x5, x6 x1,x2. Let's express the basic variables in terms of free ones:

Let us reduce the target function to next view:
Based on the obtained problem, we will form the initial simplex table:
Table 5.3
Original simplex table
Evaluative Relationships |
||||
According to definition basic solution free variables are equal to zero, and the values of the basic variables are equal to the corresponding values of the free numbers, i.e.:
Stage 3: checking the compatibility of the PAP restrictions system.
At this iteration (in Table 5.3), the sign of incompatibility of the constraint system (sign 1) is not identified (i.e., there is no line with a negative free number (except for the line objective function), in which there would not be at least one negative element (i.e., a negative coefficient for a free variable)).
At this iteration (in Table 5.3), the sign of unboundedness of the objective function (sign 2) was not identified (i.e., there is no column with a negative element in the row of the objective function (except for the column of free numbers) in which there would not be at least one positive element) .
Since the found basic solution does not contain negative components, it is admissible.
Stage 6: optimality check.
The found basic solution is not optimal, since according to the optimality criterion (sign 4) there should be no negative elements in the line of the objective function (the free number of this line is not taken into account when considering this criterion). Therefore, according to the simplex method algorithm, we move on to stage 8.
Since the found basic solution is admissible, we will search for the resolving column according to the following scheme: we determine the columns with negative elements in the row of the objective function (except for the column of free numbers). According to Table 5.3, there are two such columns: column “ x1" and column " x2" From such columns, the one that contains the smallest element in the row of the target function is selected. She will be the permissive one. Column " x2" contains the smallest element (–3) compared to the column " x1
To determine the resolving line, we find the positive estimated ratios of free numbers to the elements of the resolving column; the line that corresponds to the smallest positive evaluation ratio is accepted as resolved.
Table 5.4
Original simplex table
In Table 5.4, the smallest positive evaluative relationship corresponds to the line “ x5", therefore, it will be permissive.
The element located at the intersection of the enabling column and the enabling row is accepted as enabling. In our example, this is the element that is located at the intersection of the line “ x5" and columns " x2».
The resolving element shows one basis and one free variable that must be swapped in the simplex table to move to a new “improved” basis solution. IN in this case these are variables x5 And x2, in the new simplex table (Table 5.5) we swap them.
9.1. Transformation of the resolving element.
The resolution element of Table 5.4 is converted as follows:
![]()
We enter the resulting result into a similar cell in Table 5.5.
9.2. Resolution string conversion.
We divide the elements of the resolving row of table 5.4 by the resolving element of this simplex table, the results fit into similar cells of the new simplex table (table 5.5). Transformations of resolution string elements are given in Table 5.5.
9.3. Conversion of the resolution column.
We divide the elements of the resolution column of Table 5.4 by the resolution element of this simplex table, and the result is taken with the opposite sign. The results obtained fit into similar cells of the new simplex table (Table 5.5). Transformations of the elements of the resolution column are given in Table 5.5.
9.4. Transformation of the remaining elements of the simplex table.
The transformation of the remaining elements of the simplex table (i.e., elements not located in the resolving row and resolving column) is carried out according to the “rectangle” rule.
For example, consider transforming an element located at the intersection of the line " x3" and columns "", we will conditionally denote it " x3" In Table 5.4, we mentally draw a rectangle, one vertex of which is located in the cell whose value we are transforming (i.e. in the cell “ x3"), and the other (diagonal vertex) is in a cell with a resolving element. The other two vertices (of the second diagonal) are uniquely determined. Then the transformed value of the cell " x3" will be equal to the previous value of this cell minus the fraction, in the denominator of which is the resolving element (from Table 5.4), and in the numerator is the product of two other unused vertices, i.e.:
« x3»: .
The values of other cells are converted similarly:
« x3 x1»: ;
« x4»: ![]() ;
;
« x4 x1»: ;
« x6»: ![]() ;
;
« x6 x1»: ;
«»: ![]() ;
;
« x1»: ![]() .
.
As a result of these transformations, a new simplex table was obtained (Table 5.5).
II iteration:
Stage 1: drawing up a simplex table.
Table 5.5
Simplex tableII iterations
Estimated relationship |
||||
| ||||
|
|
Stage 2: determination of the basic solution.
As a result of the simplex transformations, a new basic solution was obtained (Table 5.5):
As you can see, with this basic solution the value of the objective function = 15, which is greater than with the previous basic solution.
The inconsistency of the system of restrictions in accordance with feature 1 in Table 5.5 has not been identified.
Stage 4: checking the boundedness of the objective function.
The unboundedness of the objective function in accordance with criterion 2 in Table 5.5 is not revealed.
Stage 5: checking the admissibility of the found basic solution.
The found basic solution in accordance with criterion 4 is not optimal, since the line of the objective function of the simplex table (Table 5.5) contains a negative element: –2 (the free number of this line is not taken into account when considering this characteristic). Therefore, we move on to stage 8.
Stage 8: determination of the resolving element.
8.1. Definition of the resolution column.
The found basic solution is acceptable; we determine the columns with negative elements in the row of the objective function (except for the column of free numbers). According to Table 5.5, there is only one such column: “ x1" Therefore, we accept it as permitted.
8.2. Definition of an enable string.
According to the obtained values of positive evaluative relations in Table 5.6, the minimum is the relation corresponding to the line “ x3" Therefore, we accept it as permitted.
Table 5.6
Simplex tableII iterations
Estimated relationship |
||||
3/1=3 – min |
||||
Stage 9: transformation of the simplex table.
Transformations of the simplex table (Table 5.6) are performed in the same way as in previous iteration. The results of transformations of elements of the simplex table are given in Table 5.7.
III iteration
Based on the results of simplex transformations of the previous iteration, we compose a new simplex table:
Table 5.7
Simplex tableIII iterations
Estimated relationship |
||||
| ||||
|
|
Stage 2: determination of the basic solution.
As a result of the simplex transformations, a new basic solution was obtained (Table 5.7):
Stage 3: checking the compatibility of the system of restrictions.
The inconsistency of the system of restrictions in accordance with feature 1 in Table 5.7 has not been identified.
Stage 4: checking the boundedness of the objective function.
The unboundedness of the objective function in accordance with criterion 2 in Table 5.7 is not revealed.
Stage 5: checking the admissibility of the found basic solution.
The found basic solution in accordance with criterion 3 is acceptable, since it does not contain negative components.
Stage 6: checking the optimality of the found basic solution.
The found basic solution in accordance with criterion 4 is not optimal, since the line of the objective function of the simplex table (Table 5.7) contains a negative element: –3 (the free number of this line is not taken into account when considering this characteristic). Therefore, we move on to stage 8.
Stage 8: determination of the resolving element.
8.1. Definition of the resolution column.
The found basic solution is acceptable; we determine the columns with negative elements in the row of the objective function (except for the column of free numbers). According to Table 5.7, there is only one such column: “ x5" Therefore, we accept it as permitted.
8.2. Definition of an enable string.
According to the obtained values of positive evaluative relations in Table 5.8, the minimum is the relation corresponding to the line “ x4" Therefore, we accept it as permitted.
Table 5.8
Simplex tableIII iterations
Estimated relationship |
||||
5/5=1 – min |
||||
Stage 9: transformation of the simplex table.
Transformations of the simplex table (Table 5.8) are performed in the same way as in the previous iteration. The results of transformations of elements of the simplex table are given in Table 5.9.
IV iteration
Stage 1: construction of a new simplex table.
Based on the results of simplex transformations of the previous iteration, we compose a new simplex table:
Table 5.9
Simplex tableIV iterations
Estimated relationship |
||||
| –(–3/5)=3/5 | |||
–(1/5)=–1/5 | ||||
| –(9/5)=–9/5 | |||
|
| –(–3/5)=3/5 |
Stage 2: determination of the basic solution.
As a result of the simplex transformations, a new basic solution was obtained; according to Table 5.9, the solution is as follows:
Stage 3: checking the compatibility of the system of restrictions.
The inconsistency of the system of restrictions in accordance with feature 1 in Table 5.9 has not been identified.
Stage 4: checking the boundedness of the objective function.
The unboundedness of the objective function in accordance with criterion 2 in Table 5.9 is not revealed.
Stage 5: checking the admissibility of the found basic solution.
The found basic solution in accordance with criterion 3 is acceptable, since it does not contain negative components.
Stage 6: checking the optimality of the found basic solution.
The found basic solution in accordance with feature 4 is optimal, since there are no negative elements in the line of the objective function of the simplex table (Table 5.9) (the free number of this line is not taken into account when considering this feature).
Stage 7: checking the alternativeness of the solution.
The solution found is unique, since there are no zero elements in the line of the objective function (Table 5.9) (the free number of this line is not taken into account when considering this characteristic).
Answer: optimal value objective function of the problem under consideration =24, which is achieved at.
Example 5.2. Solve the above linear programming problem provided that the objective function is minimized:
Solution:
I iteration:
Stage 1: formation of the initial simplex table.
Original problem linear programming is given in standard form. Let's bring it to canonical form by introducing into each of the inequality constraints an additional non-negative variable, i.e.

In the resulting system of equations, we take as allowed (basic) variables x3, x4, x5, x6, then the free variables will be x1,x2. Let us express the basic variables in terms of free ones.
Solving the ZLP using the simplex method using EXCEL tables
Let the original ZLP be reduced to canonical form, and its system of restrictions have a preferred form. For example, for the “Problem on the use of raw materials” the mathematical model of the corresponding type will be as follows:
The first simplex table on the EXCEL worksheet will look like (Fig. 10):
Assuming that the student is familiar with the algorithm of the tabular simplex method, we will describe the main stages of its implementation using EXCEL tables.
Stage 1. Select the enabling column and row and highlight the enabling element (see Fig. 11).
Stage 2. Replace the columns “Base” and “Cb” in the new table according to the rules for filling them out.

Elements of the allowing line are divided into the allowing element and written in the line corresponding to the number new table:
 , at i = r. (*)
, at i = r. (*)
All other elements of the new table are calculated using the formulas:
 , at i ≠ r (**)
, at i ≠ r (**)
where is an element of the new simplex table, a ij , - element of the previous simplex table, a rk- permitting element, a ik- element of the resolution column, a rj- element of the enabling string.
Note . To use EXCEL's ability to copy formulas with modification of the addresses of the cells included in them, it is advisable to program formulas (*) and (**) only for the cells of column “B”, giving absolute addresses to the cells that do not change. The formula data is then copied to all remaining cells in each row of the new table.
Stage 4. Elements last line of the new table are filled out either using formulas (**) or according to the rule for filling out a given row.
The results of calculations in EXCEL tables for our example are shown in Fig. 11, and the formulas used in these calculations are shown in Fig. 12.

Akulich I.L. Mathematical programming in examples and problems: Proc. manual for students economics. specialist. universities - M.: Higher. school, 1986.-319 p., ill.
Sakovich V.A. Operations Research (Deterministic Methods and Models): A Reference Guide. - Mn.: Higher. school, 1984.-256p.
Taha H. Introduction to operations research: in 2 books. Book 1. Per. from English – M.: Mir, 1985.-479 pp., ill.
Guidelines for practical exercises in the discipline “Mathematical programming” (linear programming) for students of economic specialties / Comp. Turovtsev G.V., Nudny I.P. – Zaporozhye, ZGIA, 1984.-31 p.
Mathematical programming. Lecture notes for full-time and full-time economics students correspondence departments/Glushchevsky V.V., Isaenko A.N. – Zaporozhye: ZGIA, 2003. – 150 p.
Lesson 1. Solving a linear programming problem in Excel using the Solution Search add-in
Economic and mathematical methods and models. Resource allocation problem. A classic example and solution to a linear programming problem. Description of how to use the Search for Solution add-in in Excel. The condition of the problem here is, more examples of solving problems using EMMM -#EMMM #Excel #Matprogramming #Search for a Solution #Easyhelp
Solving a linear programming problem using the add-in Search for a solution
Using the add-on Search for solutions to solve linear programming problems. Please rate it if the video was helpful to you.Simple linear programming problem #2. Simplex method for finding the maximum.
Solving a simple linear programming problem using the simplex method to find the maximum. Subtitles are available for a more detailed explanation.
.
Simple Linear Programming Problem #1. Simplex method for finding the minimum.
Solving a simple linear programming problem using the simplex method to find the minimum. Subtitles are available for further explanation.
- Simple task linear programming No. 3. Simplex method for finding the minimum.
- Solving a linear programming problem using the dual simplex method algorithm
- Solutions of direct and dual LP problems, construction dual problem LP.
- Solving a linear programming problem with non-uniform inequalities using the simplex method
- Linear programming problem with a system of equations
Lecture 2: Linear programming problem. Resource problem
The solution of a linear programming problem using the simplex method is considered.Lecture and tests at NOU INTUIT
Linear programming
Solving a linear programming problem using Finding a solution MS ExcelText material on the site is located at:
Lesson 2. Solving the dual linear programming problem in Excel
Stability analysis for direct and dual linear programming problems in Excel. See the conditions of the problem here -, more examples of problem solutions here -#Excel #mathematical programming #easyhelp
Simplex method Excel VBA (Solving a linear programming problem using macros)
Demonstration of how a macro works in Excel. Solving a linear programming problem using the Simplex method.Order a macro - [email protected]
Solution laboratory work in Excel to order
Simplex method for solving linear programming problems
linear programming. Simplex table. Permissive element. Permission string. Permissive column. Simplex relationGraphical method solving optimization problems.
A program that implements the simplex method
The program is available at the link below:Solving a transport problem in Excel using the Solution Search add-in
Linear programming problem. Transport problem. Excel solution, stability analysis. The condition of the problem is here -, more examples of solving mathematical programming problems are here -#excel #mathematical programming #Transport Problem #Linear Programming #Search for a Solution #easyhelp #Stability Analysis
Dual method
Optimization methods 12. Linear programming, simplex method
We can perform the simplex method manually
We can perform the simplex method manuallySimple linear programming problem #3. Simplex method for finding the minimum.
Very detailed solution a simple linear programming problem using the simplex method to find the minimum.Simple Linear Programming Problem #1. Simplex method for finding the minimum.
- Simple linear programming problem #2. Simplex method for finding the maximum.
- Solving a linear programming problem using the dual simplex method algorithm
- Solutions of direct, dual LP problems, construction of dual LP problems.
- Solving a linear programming problem with non-uniform inequalities using the simplex method
- Linear programming problem with a system of equations
Solving a linear programming problem by graphical method
Having built a model of a linear programming problem in the previous video lesson, it is necessary to find its solution. One of the most common optimization methods is the graphical method. It can be used if the number of unknown variables X does not exceed two. The advantages of the method include its simplicity; the disadvantages are that the accuracy of the resulting solution depends on how correctly we observed the scale during construction. Our video tutorial will teach you this.If this video brought you real benefit and you want to thank the author:
WMR: R370550256930
WMZ: Z939960413056
In our selection you can find more video tutorials on working with spreadsheets Microsoft Excel:
You can find even more other educational video tutorials on our website:
Solving linear programming problems using Excel
Optimization problems, linear programming problems, dynamic programming- solution using spreadsheetsSend your good work in the knowledge base is simple. Use the form below
Students, graduate students, young scientists who use the knowledge base in their studies and work will be very grateful to you.
Posted on http://www.allbest.ru/
Solving the problem with using Excel and simplex method
Task (distributive)
Simplex method
Solving a problem using Excel
Task (distributive)
Problem 1 (distributive)
At the enterprise, 4 types of products can be produced on 3 separate interchangeable machines.
Known:
· Production task for product release different types in the planned period
· Fund for effective working time of equipment in the planned period - ;
· Standards for the cost of machine time for the production of a unit of production - ;
· Profit in rub. from the sale of a unit of product produced on this or that equipment - .
The initial information is displayed in the table of the following form.
Table 1. Initial data
|
Fund ef. slave. time - |
Time consumption standards per unit products - profit per unit. products - |
||||
The problem requires finding a plan for distributing the production task for product output between performers
in which the task would be completed with the maximum total profit from product sales.
SOLUTION
Development of an economic and mathematical model.
The required variables characterize the volume of production by the contractor.
Then the matrix of the required variables
characterizes the plan for distributing production tasks for product output between performers.
Objective function
characterizing the total profit from the sale of all products must be maximized.
Restrictions on the availability and use of effective working time of performers will take the form of a system of linear inequalities (2):
This system of restrictions characterizes the condition that the total expenditure of effective working time by each performer in the planned period for the production of all types of products should not exceed the time fund. Thus, as a result of solving the problem, each performer will receive his own task, based on his capabilities. If in solving a problem some balancing variable takes on a value, it will characterize the underutilized effective work time from one or another contractor, which in production conditions can be used to produce products in excess of the specification.
The next block of restrictions should reflect the condition for the mandatory fulfillment of the general production task for the production of products by type and will be represented by the system linear equations (3):
Condition for non-negative variables:
Let's bring the problem to canonical form, for this we add variables to inequalities (2), and add 4 artificial bases to equalities (3). As a result, we write the mathematical model of the problem in canonical form:
Simplex method
Let's decide this task simplex method by filling out the table. The solution takes several iterations. Let's show it.
Table 1
In the most top line The coefficients of the objective function are entered in the table, the second line is the name of all the unknowns included in the simplex equations. The first column on the left contains the coefficients of the objective function, which correspond to the basic unknowns included in original program(written in the column). Next, third, column in the first simplex table- filled with the values of the basic unknowns. Next are the columns that represent the condition vectors. Their number is 19. In the next, first column after the matrix of conditions, the sums of all elements in rows are written. The column records the quotients from dividing the elements of the final column B into the elements of a certain column, a matrix of conditions. Since we have artificial basis, then in the index line there will be two calculations, in the first of them, taking into account the variables, and in the second only an artificial basis. Since we have a maximization problem, it is necessary to derive artificial bases from the basis. In the second index line, select the largest positive assessment. This is our first column. Let's find value relations
And. From these ratios we select the smallest one, for us this is the fourth row, for which the estimated ratio is equal to 1300. Select the row. The last column is the coefficient by which each element of the row is multiplied during recalculation. It is obtained by dividing the elements of the selected column by the key element, which is located at the intersection of the selected column and the row, for us it is 1. We do the recalculation for all unselected elements, which is carried out as follows: from the recalculated element we subtract the key row element, multiplied by the recalculated row coefficient: and so on for all the elements. From the basis we derive an artificial basis, while introducing a variable into the basis.
The last two lines are index lines where the values of the objective function are recalculated, as well as the entire index line, when all elements are positive or zero - the problem will be solved.
Let's show it.
table 2
Let's select the column with the variable. We find the estimated ratios, from which we select the smallest - this is 550. We derive an artificial variable from the basis, and at the same time we introduce a variable into the basis. When an artificial basis is derived from the basis, the corresponding column is removed.
Table 3
Let's select the column. The smallest estimated ratio, 600, is found in the sixth row. From the basis we derive an artificial basis, while introducing a variable into the basis.
Table 4
Let's select the column with the variable. The lowest estimated ratio, 28.57, is in the first row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 5
Let's select the column with the variable. The lowest estimated ratio, 407.7, is in the third row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 6
Let's select the column with the variable. The lowest estimated ratio, 344.3, is found in the seventh row. From the basis we derive an artificial basis, while introducing a variable into the basis.
Table 7
Let's select the column with the variable. The smallest estimated ratio, 3.273, is found in the second row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 8
Let's select the column with the variable. The smallest estimated ratio, 465, is found in the seventh row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 9
Let's select the column with the variable. The smallest estimated ratio, 109, is in the third row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 10
Let's select the column with the variable. The smallest estimated ratio, 10, is in the first row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 11
Let's select the column with the variable. The smallest estimated ratio, 147, is in the second row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 12
Let's select the column with the variable. The smallest estimated ratio, 367, is in the fifth row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 13
Let's select the column with the variable. The smallest estimated ratio, 128, is in the fourth row. We derive a variable from the basis, and we introduce a variable into the basis.
Table 14
Since there are no negative estimates in the index line, an optimal plan is obtained in which the volume of output is represented by the matrix
at the same time, the profit is maximum and amounts to 17,275.31 rubles.
Solving the problem using Excel
The mathematical model of the problem must be transferred to ET EXCEL. For this:
· Consider the organization of the initial data of the model (coefficients of the objective function and restrictions), providing them with clear names.
· Reserve independent variables of the mathematical model in separate cells.
· In one of the cells, create a formula that defines the objective function.
· Select cells and place formulas in them that correspond to the left sides of the constraints.
· Enter the menu item "Search for a solution", enter the necessary data and get optimal solution tasks.
· Analyze the resulting solution and reports.
Let's consider the sequence of actions to implement these stages of solving a problem using EXCEL.
Let's create a table for entering the initial data.
We will enter the initial data into the created form.
The coefficients of the objective function, expressing the profit from the production of a unit of each type of product (unit profit), are written in cells B6: M6.
Resource constraint coefficients that determine the need for each type of resource to produce a unit of output are located in cells B9:M15. Cells P9:P15 contain the right-hand sides of resource restrictions. For independents problem variables- cells B3:M3 are reserved for the required production volumes.
In cell N7, enter the formula for the objective function using the SUMPRODUCT function insert command:
We also fill in the restrictions on the right side.
After this, you can start looking for a solution. To solve optimization problems in EXCEL, use the SEARCH FOR SOLUTION command in the SERVICE menu.
This command operates with three main components of the optimized model built in ET:
· A cell containing the objective function of the problem.
· Variable cells containing independent variables.
· Cells containing the left parts of the restrictions on available resources, as well as simple restrictions on independent variables.
Let's consider the sequence of entering these components.
The cursor is in cell N7 and the SERVICE command - Search for a solution. A dialog box will appear on the screen.
In the window, fill in the Set target cell field, which should contain the address $N$7. Next, set the button to search for the maximum value. In the Changing cells field, enter the addresses of the desired variables $B3:$M3. Then you should enter restrictions using the Add button.
Now that all the restrictions for finding the optimal solution have been set, we can press the button:
After this we will obtain a solution to the problem.
If the calculations were successful, after completing the search for a solution, the values will be inserted into the table, and you can also specify the Report Type - Results, as a result of which we can obtain the following report. worker time equipment profit
Consequently, the solution in EXCEL is the same as with the SIMPLEX method, which means that the problem under consideration has been solved correctly.
Posted on Allbest.ru
...Similar documents
Determining the optimal volume of output mathematical method, simplex method and using Excel. Solving the problem by optimal distribution investment using applied Excel programs. Drawing up an optimal transportation scheme.
course work, added 09/10/2012
Profit planning in the production of two types of fuel. Drawing up an optimal production plan to obtain maximum profit from its sale. Determination of the basic cargo transportation plan using the minimum cost method and using Excel.
test, added 11/12/2014
Algorithm for solving linear programming problems using the simplex method. Construction of a mathematical model of a linear programming problem. Solving a linear programming problem in Excel. Finding profit and optimal production plan.
course work, added 03/21/2012
Determination, using the simplex method, of a production plan to obtain maximum profit so that type II raw materials are completely consumed. Solving linear programming problems using the Excel spreadsheet, creating an algorithm.
course work, added 09/30/2013
Study of the mathematical and economic model of the company in order to develop an optimal solution for production to obtain maximum profits and minimize costs using optimization methods and the MS Excel program and the Matlab tool package.
thesis, added 06/15/2014
Review of algorithms for solving linear programming problems. Algorithm development tabular simplex method. Drawing up a production plan that will achieve maximum sales profits. Construction of a mathematical model of the problem.
course work, added 11/21/2013
Determining the number and type of tractor and car mufflers that the company should produce in order to maximize profits. Solving linear programming problems using graphical and simplex methods using the Excel spreadsheet editor.
course work, added 04/09/2013
Optimization of costs for delivering products to consumers. Characteristic transport problem, general form solutions, generalization; meaningful and mathematical formulation of the problem, solution using MS Excel: program listing, analysis of results.
course work, added 02/04/2011
Mathematical Basics optimization. Statement of the optimization problem. Optimization methods. Solving the problem using the classical simplex method. Graphic method. Solving problems using Excel. Objective function coefficients. Linear programming, method, problems.
abstract, added 08/21/2008
Determining the quantity of purchased raw materials for production by month, throughout the year and for the year as a whole. Algorithm of necessary actions, presentation of results in graphical form. Solving the problem in a tabular form Excel processor and using VBA tools.
To solve linear programming problems simplex method in the MS Excel environment, cells are filled with source data in number mode and mathematical model formulas.
MS Excel allows you to obtain an optimal solution without limiting the dimension of the system of inequalities of the objective function.
Let’s solve the problem of manufactured products using the simplex method using the “Solution Search” add-in in MS Excel.
1. Fill in Excel spreadsheet in number mode (Fig. 1)
2. Fill out the Excel table in formula mode (Fig. 2)
Fig.1 Table in number mode

Fig.1 Table in formula mode
Here: B9:C9 – result ( optimal quantity products of each type);
В6:С6 – coefficients of the objective function;
B10 – value of the objective function;
В3:С5 – limitation coefficients;
D12:D14 – right side of restrictions;
B12:B14 – calculated (actual) values of the left side of the restrictions.
Let's solve the problem using the Data/Solution Search command. The Search for Solution dialog box appears on the screen.
In the Set target function field, a link to the active cell will be shown, i.e. on B10. Moreover, this link is absolute. In the Equal section, set the switch to Maximum (minimum) value depending on the target function. Restrictions are set using the Add button, which opens the Add Restriction input dialog box.


In the Cell Link: input field, indicate the address of the cell containing the formula on the left side of the constraint. Then the sign of the ratio is selected from the list. The Restriction field specifies the address of the cell containing right side restrictions. Click on the Add button and repeat until next limitation. After entering all restrictions, click OK.
Since all variables carry non-negativity conditions, their positivity is set through the Parameters button in the Search for a Solution dialog box. After clicking on it, the Solution Search Options window appears on the screen.

Check the Make unconstrained variables non-negative checkbox and select Solution method Search for solutions to linear problems using the simplex method. Click on the Find Solution button.
Excel will present a Solution Search Results window with a message that a solution has been found, or that it cannot find a suitable solution.
If the calculation was successful, Excel will present the following summary window. You can keep them or discard them. In addition, you can get one of three types reports (Results , Sustainability , Limits) that allow us to better understand the results obtained, including assessing their reliability.

After the solution is found, the optimal number of products of each type will appear in cells B9:C9.

When saving the report, select – Report on results (Fig. 3).
The report shows that resource 1 is not fully used by 150 kg, while resources 2 and 3 are fully used.
As a result, an optimal plan was obtained in which products of type 1 must be produced in the amount of 58 pieces, and products of type 2 in the amount of 42 pieces. At the same time, the profit from their sale is maximum and amounts to 4,660 thousand rubles.

Fig.3 Results report
1. Passenger and fast trains consisting of reserved seat, compartment and soft carriages depart daily from the formation station. The number of seats in a reserved seat car is 54, in a compartment car – 36, in a soft car – 18. The table shows the composition of each type of train and the number of cars available in the fleet various types. Determine the number of fast and passenger trains that need to be formed daily so that the number of passengers transported is maximum.
Solving transport problems
Transport problems are the tasks of determining the optimal plan for transporting cargo from given points of departure to given points of consumption.
| b 1 | b 2 | … | b k | … | b g | |
| a 1 | }
|