Meniul
AcasăiOS

Matrice de perspectivă în API-ul grafic sau diavolul este în detalii. Programare cu DirectX9: Rotirea obiectelor

Axonometria este o proiecție paralelă. Tabelul 3.3 listează mai întâi matricele proiecțiilor ortografice pe planuri de coordonate obținute din definițiile lor.

Tabelul 3.3.Matrice de transformări de proiectare și proiecție

Proiecție ortografică pe XOY

Proiecție ortografică pe YOZ

Proiecție ortografică pe XOZ

Proiecție ortografică pe planul x=p

Matricea de transformare trimetrică în planul XOY

Matricea de transformare izometrică în planul XOY

Matrice de proiecție izometrică pe planul XOY

Matrice de proiecție oblică pe XOY

Matrice de proiecție gratuită pe XOY

Matrice de proiecție a cabinetului pe XOY

Matrice de transformare a perspectivei cu un punct de fugă (planul imaginii este perpendicular pe axa x)

Matrice de transformare a perspectivei cu un punct de fugă (planul imaginii este perpendicular pe axa y)

Matrice de transformare a perspectivei cu un punct de fugă (planul imaginii este perpendicular pe axa aplicată)

Matrice de transformare a perspectivei cu două puncte de fugă (planul imaginii este paralel cu axa y)

Matrice de transformare a perspectivei cu trei puncte de fugă (planul imaginii de poziție arbitrară)

Izometria, dimetria și trimetria sunt obținute printr-o combinație de rotații urmate de o proiecție de la infinit. Dacă trebuie să descrieți proiecția pe planul XOY, atunci trebuie mai întâi să efectuați o transformare de rotație printr-un unghi relativ la axa ordonatelor, apoi la unghi raportat la axa absciselor. Tabelul 3.3 prezintă matricea de transformare trimetrică. Pentru a obține o matrice de transformare dimetrică în care, de exemplu, coeficienții de distorsiune de-a lungul axelor de abscisă și ordonate vor fi egali, relația dintre unghiurile de rotație trebuie să respecte relația

Adică prin alegerea unghiului , puteți calcula unghiul și determinați matricea de proiecție dimetrică. Pentru o transformare izometrică, relația dintre aceste unghiuri se transformă în valori strict definite, care sunt:

Tabelul 3.3 prezintă matricea de transformare izometrică, precum și matricea de proiecție izometrică pe planul XOY. Necesitatea matricelor de primul tip constă în utilizarea lor în algoritmi pentru eliminarea elementelor invizibile.

În proiecțiile oblice, liniile drepte proeminente formează cu planul de proiecție un unghi diferit de 90 de grade. Tabelul 3.3 prezintă matricea generală de proiecție oblică pe planul XOY, precum și matrice de proiecție liberă și cabinet, în care:

Proiecțiile în perspectivă (Tabelul 3.3) sunt reprezentate și de transformări de perspectivă și proiecții de perspectivă pe planul XOY. V X, V Y și V Z sunt centre de proiecție - puncte pe axele corespunzătoare. –V X, -V Y, -V Z vor fi punctele în care converg fasciculele de drepte paralele cu axele corespunzătoare.

Sistemul de coordonate al observatorului este stânga sistem de coordonate (Fig. 3.3), în care axa z e este îndreptată din punct de vedere înainte, axa x e este îndreptată spre dreapta, iar axa y e în sus. Această regulă este adoptată pentru a se asigura că axele x e și y e coincid cu axele xs și ys de pe ecran. Determinarea valorilor coordonatelor ecranului x s și y s pentru punctul P duce la necesitatea împărțirii la coordonata z e. Pentru a construi o imagine de perspectivă precisă, este necesar să se împartă la coordonatele de adâncime a fiecărui punct.

Tabelul 3.4 prezintă valorile descriptorului de vârf S(X,Y,Z) al modelului (Fig. 2.1) supus transformărilor de rotație și transformării izometrice.

Tabelul 3.4.Model de descriptori de vârf

Model original

M(R(z,90))xM(R(y,90))

Motorul nu mișcă nava. Nava rămâne pe loc, iar motorul mișcă universul în raport cu acesta.

Aceasta este foarte o parte importantă lecții, asigurați-vă că îl citiți de mai multe ori și îl înțelegeți bine.

Coordonate omogene

Până acum, am tratat vârfurile tridimensionale ca tripleți (x, y, z). Să introducem un alt parametru w și să operăm cu vectori de forma (x, y, z, w).

Amintește-ți pentru totdeauna că:

  • Dacă w == 1, atunci vectorul (x, y, z, 1) este o poziție în spațiu.
  • Dacă w == 0, atunci vectorul (x, y, z, 0) este direcția.

Ce ne oferă asta? Ok, pentru rotație acest lucru nu schimbă nimic, deoarece atât în ​​cazul rotirii punctului, cât și în cazul rotirii vectorului de direcție obțineți același rezultat. Cu toate acestea, există o diferență în cazul transferului. Translatarea vectorului de direcție va da același vector. Vom vorbi mai multe despre asta mai târziu.

Coordonatele omogene ne permit, folosind una formula matematica operați cu vectori în ambele cazuri.

Matrici de transformare

Introducere în Matrice

Cel mai simplu mod de a imagina o matrice este ca o matrice de numere, cu un număr strict definit de rânduri și coloane. De exemplu, o matrice 2x3 arată astfel:

Cu toate acestea, în Grafică 3D vom folosi doar matrice 4x4 care ne vor permite să ne transformăm vârfurile (x, y, z, w). Vârful transformat este rezultatul înmulțirii matricei cu vârful însuși:

Matrix x Vertex (în această ordine!!) = Transform. vârf

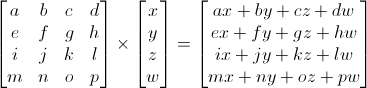
Destul de simplu. Vom folosi acest lucru destul de des, așa că este logic ca computerul să o facă:

În C++, folosind GLM:

glm::mat4 myMatrix; glm::vec4 myVector; glm:: // Atenție la comandă! El este important!

În GLSL:

mat4 myMatrix ; vec4 myVector ; // Nu uitați să completați aici matricea și vectorul cu valorile necesare vec4 transformedVector = myMatrix * myVector ; // Da, seamănă foarte mult cu GLM :)

Încercați să experimentați cu aceste fragmente.

Matricea de transfer

Matricea de transfer arată astfel:

unde X, Y, Z sunt valorile pe care vrem să le adăugăm vectorului nostru.

Deci, dacă vrem să mutăm vectorul (10, 10, 10, 1) cu 10 unități în direcția X, obținem:

... obținem (20, 10, 10, 1) un vector omogen! Amintiți-vă că 1 din parametrul w înseamnă poziție, nu direcție, iar transformarea noastră nu a schimbat faptul că lucrăm cu poziție.

Acum să vedem ce se întâmplă dacă vectorul (0, 0, -1, 0) reprezintă o direcție:

... și obținem vectorul nostru original (0, 0, -1, 0). După cum sa spus mai devreme, un vector cu parametrul w = 0 nu poate fi transferat.

Acum este momentul să îl puneți în cod.

În C++, cu GLM:

#include // după glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10,0 f, 0,0 f, 0,0 f)); glm::vec4 myVector(10,0 f, 10,0 f, 10,0 f, 0,0 f); glm::vec4 transformedVector = myMatrix * myVector ;

În GLSL:

vec4 transformedVector = myMatrix * myVector ;

De fapt, nu vei face niciodată acest lucru într-un shader, cel mai adesea vei face glm::translate() în C++ pentru a calcula matricea, o vei trece la GLSL și apoi vei efectua înmulțirea în shader.

Matrice de identitate

Aceasta este o matrice specială care nu face nimic, dar ne referim la ea, deoarece este important să ne amintim că A ori 1,0 este egal cu A:

În C++:

glm::mat4 myIdentityMatrix = glm::mat4(1.0 f);

Scaling Matrix

Arată la fel de simplu:

Deci, dacă doriți să aplicați scalarea vectorială (poziția sau direcția - nu contează) cu 2,0 în toate direcțiile, atunci aveți nevoie de:

Rețineți că w nu se modifică și, de asemenea, rețineți că matricea de identitate este caz special matrice de scalare cu un factor de scară egal cu 1 pe toate axele. De asemenea, matricea de identitate este un caz special al matricei de transfer, unde (X, Y, Z) = (0, 0, 0), respectiv.

În C++:

// adaugă #include și #include glm::mat4 myScalingMatrix = glm::scale(2,0 f, 2,0 f, 2,0 f);

Matrice de rotație

Mai complicate decât cele discutate mai devreme. Vom omite detaliile aici, deoarece nu trebuie să știți acest lucru exact pentru utilizarea zilnică. Pentru a obține mai mult informatii detaliate puteți urma linkul Întrebări frecvente Matrices and Quaternions (o resursă destul de populară și limba dvs. poate fi disponibilă acolo)

În C++:

// adaugă #include și #include glm::vec3 myRotationAxis(??, ??, ??); glm::rotate(unghi_în_grade, myRotationAxis);

Punerea laolaltă a transformărilor

Așa că acum putem roti, traduce și scala vectorii noștri. Urmatorul pas Ar fi bine să combinați transformările, care sunt implementate folosind următoarea formulă:

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector ;

ATENŢIE! Această formulă arată de fapt că scalarea se face mai întâi, apoi se face rotația și doar în sfârșit se face translația. Exact așa funcționează înmulțirea matriceală.

Asigurați-vă că vă amintiți în ce ordine se fac toate acestea, deoarece ordinea este foarte importantă, la urma urmei, puteți verifica singur:

  • Faceți un pas înainte și faceți stânga
  • Virați la stânga și faceți un pas înainte

Diferența este cu adevărat important de înțeles pentru că vei întâlni asta tot timpul. De exemplu, atunci când lucrați cu personaje de joc sau cu unele obiecte, întotdeauna scalați mai întâi, apoi rotiți și abia apoi traduceți.

De fapt, ordinea de mai sus este ceea ce aveți nevoie în general pentru personajele jocului și alte elemente: scalați-o mai întâi dacă este necesar; apoi îi stabiliți direcția și apoi îl mutați. De exemplu, pentru un model de navă (rotații eliminate pentru simplitate):

  • Direcţia greşită:
    • Mutați nava în (10, 0, 0). Centrul său este acum la 10 unități de la origine.
    • Îți ridici nava de 2 ori. Fiecare coordonată este înmulțită cu 2 „față de original”, ceea ce este departe... Deci, ajungi într-o navă mare, dar centrul ei este 2 * 10 = 20. Nu ceea ce ți-ai dorit.
  • Calea cea buna:
    • Îți ridici nava de 2 ori. Primești o navă mare, centrată la origine.
    • Îți muți nava. Este încă de aceeași dimensiune și la distanța corectă.

În C++, cu GLM:

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix ; glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector ;

În GLSL:

mat4 transform = mat2 * mat1 ; vec4 out_vec = transform * in_vec ;

Matrice de lume, vedere și proiecție

Pentru restul acestui tutorial, vom presupune că știm cum să redăm modelul 3D preferat al lui Blender, Suzanne the Monkey.

Lumea, matricele de vedere și de proiecție sunt instrument la îndemână a separa transformările.

Matricea lumii

Acest model, la fel ca triunghiul nostru roșu, este definit de un set de vârfuri, ale căror coordonate sunt date relativ la centrul obiectului, adică vârful cu coordonatele (0, 0, 0) va fi în centrul obiectului. obiect.

Apoi am dori să ne mutăm modelul pe măsură ce jucătorul îl controlează folosind tastatura și mouse-ul. Tot ce facem este să aplicăm scalarea, apoi să rotim și să traducem. Aceste acțiuni sunt efectuate pentru fiecare vârf, în fiecare cadru (efectuate în GLSL, nu în C++!) și astfel modelul nostru se deplasează pe ecran.

Acum vârfurile noastre în spațiul mondial. Acest lucru este arătat de săgeata neagră din figură. Ne-am mutat de la spațiul obiect (toate vârfurile sunt definite în raport cu centrul obiectului) la spațiul mondial (toate vârfurile sunt definite în raport cu centrul lumii).

Acest lucru este prezentat schematic astfel:

Vizualizare matrice

Pentru a cita din nou Futurama:

Motorul nu mișcă nava. Nava rămâne în același loc, iar motorul mișcă universul în jurul ei.

Încercați să vă imaginați acest lucru în legătură cu o cameră. De exemplu, dacă vrei să faci o fotografie a unui munte, nu miști camera, ci muți muntele. Acest lucru nu este posibil în viata reala, dar este incredibil de simplu în grafica computerizată.

Deci, inițial, camera dvs. se află în centrul sistemului de coordonate mondial. Pentru a muta lumea trebuie să introduceți o altă matrice. Să presupunem că doriți să mutați camera cu 3 unități la DREAPTA (+X), ceea ce este echivalentul cu mutarea întregii lumi cu 3 unități la STÂNGA (-X). În cod arată așa:

// Adăugați #include și #include glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3,0 f, 0,0 f, 0,0 f));

Din nou, imaginea de mai jos arată acest lucru în întregime. Ne-am mutat de la sistemul de coordonate mondial (toate nodurile sunt setate în raport cu centrul sistemului mondial) la sistemul de coordonate al camerei (toate nodurile sunt setate în raport cu camera):

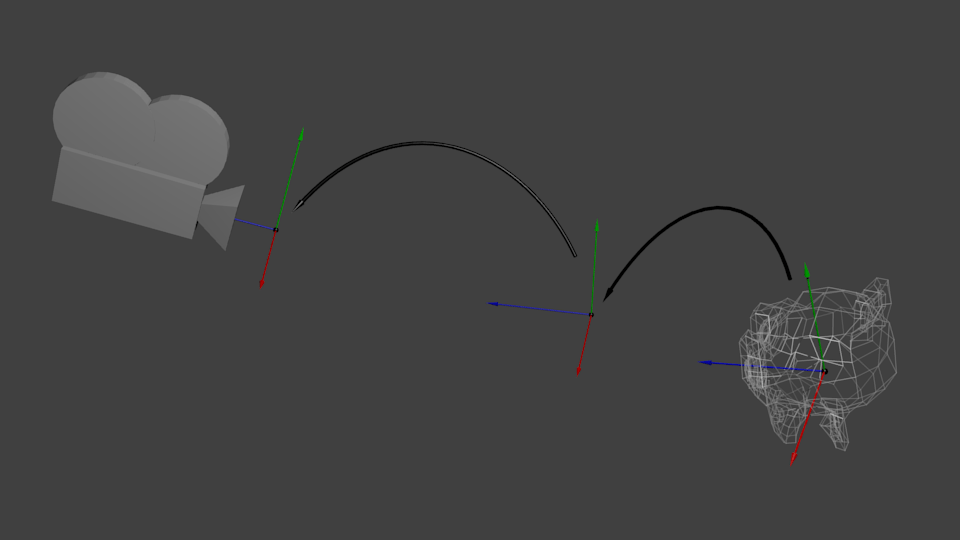
Și în timp ce creierul tău digeră acest lucru, vom arunca o privire la funcția pe care ne-o oferă GLM, mai precis glm::LookAt:

glm::mat4 CameraMatrix = glm::LookAt(cameraPosition, // Poziția camerei în spațiul mondial cameraTarget // Indică unde căutați în spațiul mondial upVector // Un vector care indică direcția ascendentă. De obicei (0, 1, 0));

Și iată o diagramă care arată ce facem:

Totuși, acesta nu este sfârșitul.

Matricea de proiecție

Deci acum suntem în spațiul camerei. Aceasta înseamnă că un vârf care primește coordonatele x == 0 și y == 0 va fi afișat în centrul ecranului. Cu toate acestea, atunci când se afișează un obiect, distanța până la cameră (z) joacă, de asemenea, un rol important. Pentru două vârfuri cu același x și y, vârful cu o valoare z mai mare va apărea mai aproape decât celălalt.

Aceasta se numește proiecție în perspectivă:

Și, din fericire pentru noi, o matrice 4x4 poate face această proiecție:

// Creează o matrice foarte greu de citit, dar este totuși o matrice standard 4x4 glm::mat4 projectionMatrix = glm::perspectivă (glm::radiani (FoV), // Câmp de vedere vertical în radiani. De obicei, între 90° (foarte lat) și 30° (îngust) 4,0 f/3,0 f // Raportul de aspect. Depinde de dimensiunea ferestrei tale. Rețineți că 4/3 == 800/600 == 1280/960 0,1 f // Aproape de planul de tăiere. Trebuie să fie mai mare decât 0. 100.0f // Plan de tăiere departe.);

Ne-am mutat de la Camera Space (toate nodurile sunt definite în raport cu camera) la Homogenous Space (toate nodurile sunt într-un cub mic. Tot ceea ce este în interiorul cubului este afișat pe ecran).

Acum să ne uităm la următoarele imagini, pentru a putea înțelege mai bine ce se întâmplă cu proiecția. Înainte de proiecție, avem obiecte albastre în spațiul camerei, în timp ce figura roșie arată vederea camerei, adică tot ceea ce vede camera.

Utilizarea matricei de proiecție dă următorul efect:

În această imagine, vederea camerei este un cub și toate obiectele sunt deformate. Obiectele care sunt mai aproape de cameră par mari, iar cele care sunt mai departe par mici. Exact ca in realitate!

Iată cum va arăta:

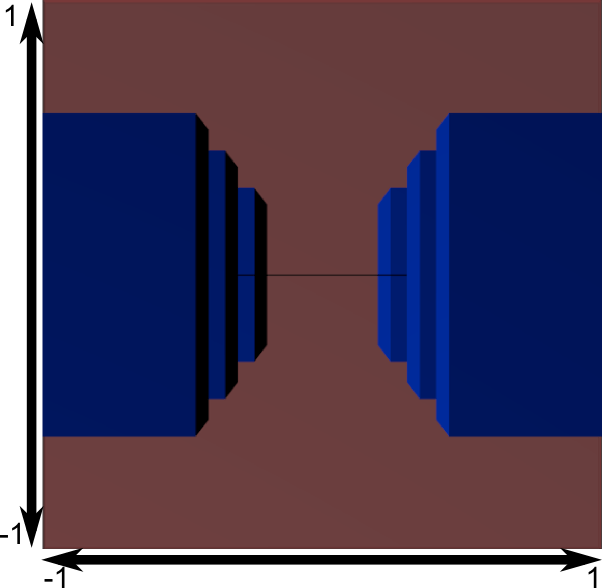
Imaginea este pătrată, deci se aplică următoarele transformări matematice pentru a întinde imaginea în funcție de dimensiunile actuale fereastră:

Și această imagine este ceea ce va fi de fapt rezultat.

Combinarea transformărilor: matricea ModelViewProjection

... Doar transformările matrice standard pe care deja le iubiți!

// C++ : calcul matrice glm::mat4 MVPmatrix = proiectie * vizualizare * model ; // Tine minte! ÎN ordine inversă!

// GLSL: Aplicați Matrix transformed_vertex = MVP * in_vertex ;

Punând totul împreună

  • Primul pas este crearea matricei noastre MVP. Acest lucru trebuie făcut pentru fiecare model pe care îl afișați.

// Matrice de aruncare: câmp vizual de 45°, raport de aspect 4:3, interval: 0,1 unitate<->100 de unitati glm::mat4 Projection = glm::perspective(glm::radiani(45,0 f), 4,0 f / 3,0 f, 0,1 f, 100,0 f); // Sau, pentru ortocamera glm::mat4 View = glm::lookAt(glm::vec3(4, 3, 3), // Camera este în coordonatele lumii (4,3,3) glm::vec3(0, 0, 0), // Şi îndreptată spre origine glm::vec3(0, 1, 0) // „Capul” este deasupra); // Matricea modelului: matricea identității (Modelul este la origine) glm::mat4 Model = glm::mat4(1.0 f); // Individual pentru fiecare model // Matricea finală ModelViewProjection, care este rezultatul înmulțirii celor trei matrice ale noastre glm::mat4 MVP = Projection * View * Model ; // Amintiți-vă că înmulțirea matricei se face în ordine inversă

  • Al doilea pas este să transmiteți acest lucru către GLSL:

// Obține mânerul variabilei în shader // O singură dată în timpul inițializării. GLuint MatrixID = glGetUniformLocation(ID program, „MVP”); // Treceți transformările noastre la shaderul curent // Acest lucru se face în bucla principală, deoarece fiecare model va avea o matrice MVP diferită (cel puțin partea M) glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);

  • Al treilea pas este să folosim datele primite în GLSL pentru a ne transforma vârfurile.

// Date de intrare Vertex, diferite pentru toate execuțiile acestui shader. layout (locație = 0) în vec3 vertexPosition_modelspace ; // Valori care rămân constante pe întreaga plasă. uniform mat4 MVP ; void main ()( // Poziția de ieșire a vârfului nostru: MVP * poziție gl_Position = MVP * vec4(vertexPosition_modelspace, 1); )

  • Gata! Acum avem același triunghi ca în Lecția 2, încă situat la origine (0, 0, 0), dar acum îl vedem în perspectivă din punctul (4, 3, 3).

În Lecția 6, veți învăța cum să schimbați aceste valori în mod dinamic folosind tastatura și mouse-ul pentru a crea camera pe care obișnuiți să o vedeți în jocuri. Dar mai întâi, vom învăța cum să oferim modelelor noastre culori (Lecția 4) și texturi (Lecția 5).

Sarcini

  • Încercați să schimbați valorile glm::perspective
  • În loc să utilizați proiecția în perspectivă, încercați să utilizați ortogonal (glm:ortho)
  • Modificați ModelMatrix pentru a muta, roti și scala triunghiul
  • Utilizați sarcina anterioară, dar cu în ordine diferită operațiuni. Acordați atenție rezultatului.

La un moment dat, orice dezvoltator din domeniu grafica pe computer Apare întrebarea: cum funcționează aceste matrici promițătoare? Uneori, răspunsul este foarte greu de găsit și, așa cum se întâmplă de obicei, majoritatea dezvoltatorilor renunță la jumătatea sarcinii.

Aceasta nu este o soluție la problemă! Să ne dăm seama împreună!

Să fim realiști cu o părtinire practică și să luăm ca subiect de testare versiuni OpenGL 3.3. Pornind de la această versiune, fiecare dezvoltator trebuie să implementeze modulul în mod independent operații cu matrice. Grozav, de asta avem nevoie. Să ne descompunem sarcina dificilă și să evidențiem punctele principale. Câteva fapte din specificația OpenGL:

  • Matricele sunt stocate în coloane (coloană-major);
  • Coordonate omogene;
  • Volum de tăiere canonic (CVV) într-un sistem de coordonate pentru stânga.
Există două moduri de a stoca matrice: coloană-major și rând-major. În cursurile de algebră liniară se folosește schema de rânduri majore. De în general Reprezentarea matricelor în memorie nu contează, deoarece o matrice poate fi întotdeauna convertită dintr-o reprezentare în alta prin simplă transpunere. Și, deoarece nu există nicio diferență, atunci pentru toate calculele ulterioare vom folosi matrice clasice de rânduri majore. La programarea OpenGL există mic truc, care vă permite să refuzați transpunerea matricelor menținând în același timp calculele clasice de rânduri majore. Matricea trebuie transferată în programul shader așa cum este, iar în shader multiplicarea trebuie efectuată nu între un vector și o matrice, ci între o matrice și un vector.

Coordonatele omogene nu sunt un sistem foarte complicat cu un număr de reguli simple la conversia coordonatelor carteziene convenţionale în coordonate omogene şi invers. O coordonată omogenă este o matrice de rând de dimensiune. Pentru a converti o coordonată carteziană într-o coordonată omogenă, este necesar X, yȘi z inmultiti cu oricare numar real w(cu excepția lui 0). Apoi, trebuie să scrieți rezultatul în primele trei componente, iar ultima componentă va fi egală cu multiplicatorul w. Cu alte cuvinte:
- coordonate carteziene
w– număr real nu este egal cu 0

- coordonate omogene

Un mic truc: Dacă w este egal cu unu, atunci tot ceea ce este necesar pentru traducere este transferul componentelor X, yȘi zși atribuiți unul ultimei componente. Adică, obțineți o matrice de rând:

Câteva cuvinte despre calitate zero w. Din punctul de vedere al coordonatelor omogene, acest lucru este destul de acceptabil. Coordonatele omogene vă permit să faceți distincția între puncte și vectori. Într-un sistem de coordonate carteziene, o astfel de împărțire este imposibilă.

- punctul în care ( x, y, z) – Coordonate carteziene

- vector, unde ( x, y, z) – vector rază

Translația inversă a unui vârf din coordonatele omogene în coordonatele carteziene se realizează după cum urmează. Toate componentele unei matrice de rânduri trebuie împărțite la ultima componentă. Cu alte cuvinte:

- coordonate omogene
- coordonate carteziene

Principalul lucru pe care trebuie să-l știți este că toți algoritmii de tăiere și rasterizare OpenGL funcționează în coordonate carteziene, dar înainte de asta toate transformările sunt efectuate în coordonate omogene. Trecerea de la coordonatele omogene la coordonatele carteziene se realizează în hardware.

Volumul canonic de tăiere (CVV) este una dintre părțile cel mai puțin documentate ale OpenGL. După cum se poate observa din fig. 1 CVV este un cub aliniat pe axă centrat la origine și cu o lungime a muchiei egală cu două. Tot ceea ce se încadrează în zona CVV este supus rasterizării, tot ceea ce este în afara CVV este ignorat. Orice lucru care intră parțial în afara CVV este supus algoritmilor de tăiere. Cel mai important lucru pe care trebuie să-l știți este că sistemul de coordonate CVV este stângaci!


Orez. 1. Volum de tăiere canonic OpenGL (CVV)

Sistem de coordonate pentru stângaci? Cum poate fi acest lucru, deoarece specificația pentru OpenGL 1.0 afirmă clar că sistemul de coordonate folosit este dreptaci? Să ne dăm seama.


Orez. 2. Sisteme de coordonate

După cum se poate observa din fig. Cele 2 sisteme de coordonate diferă doar în direcția axei Z. OpenGL 1.0 folosește de fapt dreptaci sistem utilizator coordonate Dar sistemul de coordonate CVV și sistemul de coordonate utilizator sunt două lucruri complet diferite. Mai mult decât atât, începând cu versiunea 3.3, nu mai există așa ceva ca sistem standard Coordonatele OpenGL. După cum am menționat mai devreme, programatorul însuși implementează modulul de operații cu matrice. Formarea matricelor de rotație, formarea matricelor de proiecție, căutarea unei matrici inverse, înmulțirea matricelor sunt set minim operațiuni incluse în modulul operațiuni matriceale. Apar două întrebări logice. Dacă volumul de vizibilitate este un cub cu o lungime a muchiei egală cu două, atunci de ce este vizibilă pe ecran o scenă cu dimensiuni de câteva mii de unități? În ce moment se transformă sistemul de coordonate utilizator în sistemul de coordonate CVV? Matricele de proiecție sunt tocmai entitatea care se ocupă de aceste probleme.

Ideea principală a celor de mai sus este că dezvoltatorul însuși este liber să aleagă tipul de sistem de coordonate al utilizatorului și trebuie să descrie corect matricele de proiecție. Acest lucru completează faptele despre OpenGL și este timpul să punem totul împreună.

Una dintre cele mai comune și mai greu de înțeles matrice este matricea de transformare a perspectivei. Deci, cum se raportează la CVV și sistemul de coordonate al utilizatorului? De ce obiectele devin mai mici pe măsură ce distanța lor față de observator crește? Pentru a înțelege de ce obiectele se micșorează pe măsură ce distanța crește, să ne uităm la transformările matriceale ale unui model 3D pas cu pas. Nu este un secret pentru nimeni că orice model tridimensional constă dintr-o listă finită de vârfuri care suferă transformări de matrice complet independent unul de celălalt. Pentru a determina coordonatele unui vârf tridimensional pe un ecran de monitor bidimensional, trebuie să:

  1. Convertiți coordonatele carteziene în coordonate omogene;
  2. Înmulțiți coordonatele omogene cu matricea modelului;
  3. Rezultatul este înmulțit cu matricea de vizualizare;
  4. Înmulțiți rezultatul cu matricea de proiecție;
  5. Convertiți rezultatul din coordonate omogene în coordonate carteziene.
Conversia coordonatelor carteziene în coordonate omogene a fost discutată mai devreme. Sensul geometric al matricei modelului este de a traduce modelul din sistem local coordonate în sistem global coordonate Sau, după cum se spune, mutați vârfurile din spațiul model în spațiul mondial. Să spunem simplu, un obiect tridimensional încărcat dintr-un fișier este situat în spațiul model, unde coordonatele sunt măsurate în raport cu obiectul însuși. Apoi, folosind matricea modelului, modelul este poziționat, scalat și rotit. Ca rezultat, toate nodurile modelului 3D primesc coordonate omogene reale în scena 3D. Spațiul model în raport cu spațiul mondial este local. Din spațiul model, coordonatele sunt transferate în spațiul mondial (de la local la global). În acest scop, se utilizează o matrice model.

Acum să trecem la pasul trei. Aici intervine spațiul de vedere. În acest spațiu, coordonatele sunt măsurate în raport cu poziția și orientarea observatorului ca și cum el ar fi centrul lumii. Spațiul de vizualizare este local în raport cu spațiul mondial, deci coordonatele trebuie introduse în el (și nu scoase, ca în cazul precedent). Transformarea directă a matricei elimină coordonatele dintr-un anumit spațiu. Pentru a le introduce în ea, dimpotrivă, este necesară inversarea transformării matriceale, de aceea transformarea de tip este descrisă de matricea inversă. Cum să obții asta matrice inversă? Mai întâi, să obținem matricea observatorului direct. Ce caracterizează un observator? Observatorul este descris de coordonatele în care se află și de vectorii direcției de vizualizare. Observatorul privește întotdeauna în direcția axei sale locale Z. Observatorul se poate deplasa în jurul scenei și se poate întoarce. În multe privințe, aceasta seamănă cu sensul matricei modelului. În mare, așa stau lucrurile. Cu toate acestea, pentru un observator, operația de scalare este lipsită de sens, prin urmare, un semn egal nu poate fi pus între matricea model a observatorului și matricea model a unui obiect tridimensional. Matricea model a observatorului este matricea directă dorită. Prin inversarea acestei matrice, obținem matricea de vedere. În practică, aceasta înseamnă că toate vârfurile din coordonatele omogene globale vor primi noi coordonate omogene în raport cu observatorul. În consecință, dacă observatorul a văzut un anumit vârf, atunci valoarea coordonatei omogene z a unui punct dat în spațiul de vizualizare va fi cu siguranță un număr pozitiv. Dacă vârful era în spatele observatorului, atunci valoarea coordonatei sale omogene zîn spațiul de vizualizare va fi cu siguranță un număr negativ.

Pasul patru este cel mai interesant pas. Etapele anterioare au fost discutate atât de detaliu în mod intenționat, astfel încât cititorul să aibă o imagine completă a tuturor operanzilor din pasul al patrulea. La a patra etapă, coordonatele omogene sunt transferate din spațiul de vizualizare în spațiul CVV. Încă o dată, se subliniază faptul că toate vârfurile potențial vizibile vor avea o valoare pozitivă a coordonatei omogene. z.

Luați în considerare o matrice de forma:

Și un punct din spațiul omogen al observatorului:

Să înmulțim coordonata omogenă cu matricea în cauză:

Să convertim coordonatele omogene rezultate în coordonate carteziene:

Să presupunem că există două puncte în spațiul de vedere cu aceleași coordonate XȘi y, dar cu coordonate diferite z. Cu alte cuvinte, unul dintre puncte este în spatele celuilalt. Din cauza distorsiunii perspectivei, observatorul trebuie să vadă ambele puncte. Într-adevăr, reiese clar din formulă că datorită împărțirii prin coordonate z, compresia are loc la punctul de origine. Cum mai multă valoare z(cu cât punctul este mai departe de observator), cu atât compresia este mai puternică. Aceasta este explicația efectului de perspectivă.

Specificația OpenGL afirmă că operațiunile de tăiere și rasterizare sunt efectuate în coordonate carteziene, iar procesul de conversie a coordonatelor omogene în coordonate carteziene se realizează automat.

Matricea (1) este un șablon pentru o matrice de proiecție în perspectivă. După cum sa menționat mai devreme, sarcina matricei de proiecție constă din două puncte: stabilirea unui sistem de coordonate utilizator (stângaci sau dreptaci), transferarea volumului de vizibilitate al observatorului către CVV. Să derivăm o matrice de perspectivă pentru un sistem de coordonate de utilizator stângaci.

Matricea de proiecție poate fi descrisă folosind patru parametri (Fig. 3):

  • Unghiul de vizualizare în radiani ( fovy);
  • Raport de aspect ( aspect);
  • Distanța până la cel mai apropiat plan de tăiere ( n);
  • Distanța până la planul de tăiere îndepărtat ( f).


Orez. 3. Perspectivă volum de vizibilitate

Să luăm în considerare proiecția unui punct din spațiul observatorului pe marginea frontală a decupării volumului de vizibilitate în perspectivă. Pentru o mai mare claritate, în fig. 4 prezintă o vedere laterală. De asemenea, trebuie luat în considerare faptul că sistemul de coordonate utilizator coincide cu sistemul de coordonate CVV, adică sistemul de coordonate stânga este folosit peste tot.


Orez. 4. Proiectarea unui punct arbitrar

Pe baza proprietăților triunghiurilor similare, următoarele egalități sunt adevărate:

Să exprimăm yꞌ și xꞌ:

În principiu, expresiile (2) sunt suficiente pentru a obține coordonatele punctelor de proiecție. Cu toate acestea, pentru a ecraniza corect obiectele tridimensionale, trebuie să cunoașteți adâncimea fiecărui fragment. Cu alte cuvinte, este necesară stocarea valorii componentei z. Aceasta este valoarea folosită pentru testele de adâncime OpenGL. În fig. 3 este clar că valoarea zꞌ nu este potrivit ca adâncime a fragmentului, deoarece toate proiecțiile punctuale pot aceeași valoare zꞌ. Calea de ieșire din această situație este folosirea așa-numitei pseudo-adâncimi.

Proprietăți de pseudoadâncime:

  1. Pseudo-adâncimea este calculată pe baza valorii z;
  2. Cu cât punctul este mai aproape de observator, cu atât pseudoadâncimea are mai puțină valoare;
  3. Toate punctele situate pe planul frontal al volumului de vizibilitate au o valoare pseudo-adâncime de -1;
  4. Toate punctele situate pe planul de tăiere îndepărtat al volumului de vizibilitate au o valoare pseudo-adâncime de 1;
  5. Toate fragmentele aflate în interiorul volumului de vizibilitate au o valoare pseudo-adâncime în intervalul [-1 1].
Să derivăm formula prin care se va calcula pseudo-adâncimea. Să luăm ca bază următoarea expresie:

Cote AȘi b trebuie calculat. Pentru a face acest lucru, folosim proprietățile pseudoadâncimii 3 și 4. Obținem un sistem de două ecuații cu două necunoscute:

Să adăugăm ambele părți ale sistemului și să înmulțim rezultatul cu produsul fn, în care fȘi n nu poate fi egal cu zero. Primim:

Să deschidem parantezele și să rearanjam termenii astfel încât doar partea cu A, iar în dreapta doar cu b:

Să înlocuim (6) în (5). Să transformăm expresia într-o fracție simplă:

Înmulțiți ambele părți cu -2fn, în care fȘi n nu poate fi egal cu zero. Să prezentăm altele asemănătoare, rearanjam termenii și exprimăm b:

Să substituim (7) în (6) și să exprimăm A:

În consecință componentele AȘi b sunt egale:

Acum să substituim coeficienții obținuți în matricea piesei de prelucrat (1) și să vedem ce se întâmplă cu coordonatele z pentru un punct arbitrar din spațiul omogen al observatorului. Înlocuirea se realizează după cum urmează:

Lăsați distanța până la planul frontal de tăiere n este egală cu 2 și distanța până la planul îndepărtat de tăiere f este egal cu 10. Luați în considerare cinci puncte din spațiul omogen al observatorului:

Aranjament reciproc puncte și volum de vizibilitate
Punct Sens Descriere
1 1 Punctul este situat în fața planului de tăiere frontal al volumului de vizibilitate. Nu trece rasterizarea.
2 2 Punctul este situat pe marginea frontală a decupării volumului de vizibilitate. În curs de rasterizare.
3 5 Punctul este situat între marginea de tăiere frontală și marginea de tăiere îndepărtată a volumului de vizibilitate. În curs de rasterizare.
4 10 Punctul este situat pe marginea îndepărtată a limitei volumului vizibilității. În curs de rasterizare.
5 20 Punctul este situat dincolo de marginea îndepărtată a limitei de volum de vizibilitate. Nu trece rasterizarea.

Să înmulțim toate punctele cu matricea (8), apoi să convertim coordonatele omogene rezultate în coordonate carteziene . Pentru a face acest lucru, trebuie să calculăm valorile noilor componente omogene Și .
Punctul 1:

Rețineți că coordonatele omogene poziționat absolut corect în CVV și, cel mai important, testul de adâncime OpenGL este acum posibil, deoarece pseudo-adâncimea satisface pe deplin cerințele testului.

Cu coordonata z Ne-am dat seama, să trecem la coordonate XȘi y. După cum am menționat mai devreme, întregul volum de vizibilitate în perspectivă trebuie să se încadreze în CVV. Lungimea marginii CVV este de două. În consecință, înălțimea și lățimea volumului de vizibilitate în perspectivă trebuie să fie comprimate la două unități convenționale.

Avem la dispoziție un colț fovyși magnitudinea aspect. Să exprimăm înălțimea și lățimea folosind aceste valori.


Orez. 5. Volumul vizibilității

Din fig. 5 este clar că:

Acum poți obține privire finală matrice de proiecție în perspectivă pentru un sistem de coordonate pentru stângaci personalizat care funcționează cu CVV OpenGL:

Aceasta completează derivarea matricelor.

Câteva cuvinte despre DirectX - principalul concurent al OpenGL. DirectX diferă de OpenGL doar prin dimensiunile CVV-ului și poziționarea acestuia. În DirectX, CVV este un paralelipiped dreptunghic cu lungimi de-a lungul axelor sale XȘi y egal cu doi și de-a lungul axei z lungimea este egală cu unu. Gamă XȘi y este [-1 1], iar intervalul z egal cu . În ceea ce privește sistemul de coordonate CVV, DirectX, ca și OpenGL, utilizează un sistem de coordonate stângaci.

Pentru a afișa matrice de perspectivă pentru un sistem de coordonate personalizat pentru dreapta, trebuie să redesenați Fig. 2, Fig. 3 și Fig. 4 ținând cont de noua direcție a axei Z. Calculele ulterioare sunt complet similare, până la semn. Pentru matricele DirectX, proprietățile de pseudo-adâncime 3 și 4 sunt modificate pentru a se potrivi cu intervalul.

În acest moment, subiectul matricelor promițătoare poate fi considerat închis.

Pentru a descrie în detaliu metodele de urmărire a caracteristicilor punctuale, calibrarea camerei și reconstrucția obiectelor 3D, este necesar să se introducă un model de proiectare în perspectivă și să se descrie proprietățile geometrice ale acestei transformări. Punctele mai multor imagini obținute folosind proiecția în perspectivă au relații speciale între ele, care sunt descrise de geometria epipolară. Modelele acestor relaţii trebuie examinate în detaliu, deoarece Aproape toate metodele de reconstrucție tridimensională necesită evaluarea modelelor corespunzătoare și se bazează pe proprietățile acestora.

Este necesar să se noteze separat ipoteza că toate imaginile sursă captează aceeași scenă, de exemplu. fiecare imagine este o vedere a scenei de la o anumită cameră. Prin urmare, pentru comoditatea descrierii, este introdus conceptul de vedere, ca o imagine cu un model de cameră asociat din care a fost obținută.

Proiecția în perspectivă

Modelul de proiecție în perspectivă corespunde unei camere pinhole ideală. Acest model se potrivește destul de mult cu procesul de construire a imaginii în majoritatea camerelor foto și video moderne. Cu toate acestea, din cauza limitărilor opticii moderne, procesul real este oarecum diferit de modelul camerei pinhole. Diferențele dintre procesul real și model se numesc distorsiuni și sunt modelate separat.

Modelul celei mai simple camere pinhole este convenabil prin faptul că este complet descris de centrul de proiecție și poziția planului imaginii. Prin urmare, proiecția oricărui punct al scenei din imagine poate fi găsită ca intersecția razei care conectează centrul proiecției și punctul scenei cu planul imaginii.

Cel mai simplu model de proiecție în perspectivă

Să luăm în considerare cel mai simplu caz când centrul proiecției camerei (focalizare) este plasat la originea sistemului de coordonate, iar planul imaginii coincide cu planul Z=1. Fie (X,Y,Z) coordonatele unui punct din spațiul tridimensional și (x,y) proiecția acestui punct pe imaginea I. Proiecția în perspectivă în acest caz este descrisă de următoarele ecuații:

Sub formă de matrice folosind coordonate omogene, aceste ecuații sunt rescrise după cum urmează:

(2.2)

Planul situat la o distanță de 1 de centrul proiecției și perpendicular pe axa optică se numește plan ideal al imaginii. Axa optică intersectează planul ideal al imaginii într-un punct c, numit punct principal. O ilustrare a celui mai simplu caz de proiecție în perspectivă este prezentată în Fig. 1.

Calibrare internă a camerei

Cel mai simplu caz de proiecție în perspectivă aproape întotdeauna nu corespunde cu camera reală. Distanța de la centrul de proiecție la planul imaginii, de ex. distanța focală, notată cu f, nu este de obicei egală cu 1. De asemenea, coordonatele unui punct din planul imaginii pot să nu coincidă cu coordonatele absolute. Folosind camera digitala, relația dintre coordonatele unui punct din imagine și coordonatele absolute ale unui punct pe un plan ideal, este determinată de forma și dimensiunea pixelilor matricei.

Să notăm dimensiunile pixelilor matricei camerei digitale ca p x , p y , unghiul de înclinare a pixelilor ca α și punctul principal ca , Fig. 2. Atunci coordonatele punctului (x,y) din imagine corespunzătoare punctului (x R , y R) din planul ideal sunt determinate de expresia:

(2.3)

Dacă f x ,f y este distanța focală f, măsurată în lățimi și înălțimi ale pixelilor, iar tan(α)*f/p y este notat cu s, atunci formula 2.3 se transformă în:

(2.4)

Matricea K se numește matricea de calibrare internă a camerei. În cele mai multe cazuri, în camerele digitale reale unghiul pixelilor este aproape drept, de exemplu. parametrul s=0, iar lățimea și înălțimea pixelului sunt egale. Punctul principal este de obicei situat în centrul imaginii. Prin urmare, matricea K poate fi scrisă ca:

(2.5)

Această ipoteză despre forma matricei K este utilizată pe scară largă pentru a simplifica algoritmii pentru determinarea calibrării interne a camerei, precum și în modelarea imaginilor sintetice necesare pentru a evalua calitatea și eficiența metodelor de reconstrucție 3D.

Calibrarea camerei externe

Fie M un punct de scenă în spațiul tridimensional. Orice mișcare este o transformare euclidiană a spațiului, prin urmare în coordonate omogene se exprimă astfel:

(2.6)

unde R este matricea de rotație, T= T este vectorul de translație.

Mișcarea camerei în raport cu scenă este echivalentă cu mișcarea inversă a punctelor scenei față de cameră, prin urmare este egală cu:

(2.7)

unde R, T este matricea de rotație și vectorul de mișcare a camerei în raport cu scena. Matricea C se numește matrice calibrare externă camere de luat vederi. Matricea C -1 se numește matrice mișcările camerei. Astfel, matricea de calibrare externă a camerei transpune coordonatele punctelor scenei din sistemul de coordonate al scenei în sistemul de coordonate asociat camerei.

Model complet de proiecție în perspectivă

Din expresiile 2.1, 2.4, 2.7, putem deriva o expresie pentru o proiecție în perspectivă arbitrară pentru orice cameră cu o orientare și o poziție arbitrară în spațiu:

Într-o formă mai concisă, ținând cont de notația anterioară, această formulă poate fi scrisă astfel:

Matricea P se numește matricea de proiecție a camerei.

Prin analogie cu transformarea de perspectivă generală, să considerăm mai întâi cel mai simplu caz de transformare în perspectivă a unui plan. Fie planul p să coincidă cu planul Z=0, atunci coordonatele tridimensionale omogene ale oricăruia dintre punctele sale sunt M=. Pentru orice cameră cu o matrice de proiecție P, transformarea în perspectivă a planului este descrisă de o matrice 3*3:


Deoarece orice plan din spațiul tridimensional poate fi transferat în planul Z = 0 prin transformarea euclidiană de rotație și translație, ceea ce este echivalent cu înmulțirea matricei camerei P cu matricea de transformare L, atunci afișarea în perspectivă a unui plan arbitrar în spațiul este descris de transformare liniară cu o matrice 3*3.

Se mai numește și transformarea planului de perspectivă omografie. Sub formă de matrice, transformarea în perspectivă a planului se scrie ca m=HM.

Geometria a două imagini

Scena capturată pe toate imaginile sursă este considerată nemișcată, prin urmare poziția relativă a proiecțiilor punctelor scenei pe diferite cadre nu se poate modifica la întâmplare. Restricțiile impuse locației proiecțiilor punctuale depind, evident, de parametrii camerelor și de poziția acestora unul față de celălalt. Prin urmare, determinarea modelelor de astfel de restricții oferă câteva informații despre pozițiile relative ale camerelor de la care au fost obținute imaginile.

Transformarea planului de perspectivă

Dacă centrele celor două camere coincid, atunci punctele de pe planurile imaginii ambelor camere sunt translate unul în celălalt printr-o transformare în perspectivă a planului. În acest caz, transformarea punctelor între imagini nu depinde de forma scenei tridimensionale, ci depinde doar de poziția relativă a planurilor imaginii.

Dacă întreaga scenă sau o parte a acesteia este un avion, atunci imaginile sale sunt activate tipuri diferite cu centrele camerelor necoincidente pot fi convertite unul în altul printr-o transformare de omografie. Fie p planul observat, H 1 transformarea omografică dintre planul p și imagine eu 1, H 2 - transformare omografică între planul p şi imagine eu 2. Apoi transformarea omografică H 12 între imagini eu 1Și eu 2 poate fi scos după cum urmează:

H 12 nu depinde de parametrizarea planului p și, prin urmare, nu depinde de sistemul de coordonate din spațiu

Majoritatea metodelor de determinare a coordonatelor punctelor 3D din proiecțiile lor și metodele de reconstrucție a unei scene 3D se bazează pe presupunerea că centrul camerei se mișcă între vederi. Prin urmare, dacă centrele camerelor de mai multe tipuri coincid, aceste metode vor da rezultate incorecte. Astfel de configurații ale camerei trebuie detectate și tratate într-un mod special.

Deoarece transformarea omografică este scrisă în coordonate omogene, matricea H este definită la scară. Are 8 grade de libertate și este parametrizată de 8 variabile. Fiecare pereche cunoscută de puncte corespunzătoare m 1Și m 2în prima și respectiv a doua imagine dă 2 ecuatii lineare din elementele matricei H. Prin urmare, 4 perechi cunoscute de puncte corespunzătoare sunt suficiente pentru a alcătui un sistem de ecuații liniare de 8 ecuații cu 8 necunoscute. Conform acestui sistem, omografia H poate fi determinată în mod unic dacă niciunul dintre puncte nu se află pe aceeași linie.

Matricea fundamentală

Să luăm în considerare cazul în care centrele celor două tipuri de camere nu coincid. Lăsa C 1Și C 2- centrele a două camere, M - punctul tridimensional al scenei, m 1Și m 2- proiecțiile punctului M pe prima și, respectiv, pe a doua imagine. Fie P un plan care trece prin punctul M și centrele camerelor C 1Și C 2. Planul P intersectează planurile imaginii primei și celei de-a doua vederi de-a lungul liniilor drepte l 1Și l 2. Din moment ce razele C 1 MȘi C 2 M se află în planul P, atunci este evident că punctele m 1Și m 2 culcați pe linii drepte l 1Și l 2 respectiv. Poți să dai mai mult afirmație generală că proiecțiile oricărui punct M" aflat în planul P pe ambele imagini trebuie să se afle pe linii drepte l 1Și l 2. Aceste linii se numesc linii epipolare. Planul P se numește plan epipolar.

Două vederi ale aceleiași scene sunt numite pereche stereo și segment C 1 C 2, conectarea centrelor camerelor se numește baza perechii stereo (linia de bază) sau bază stereo. Orice plan epipolar trece prin segment C 1 C 2. Lăsa C 1 C 2 intersectează prima și a doua imagine în puncte e 1Și e 2 respectiv. Puncte e 1Și e 2 se numesc puncte epipolare sau epipoli. Toate liniile epipolare se intersectează în puncte e 1Și e 2în prima și respectiv a doua imagine. Setul de planuri epipolare este un fascicul care se intersectează de-a lungul bazei stereo C 1 C 2. Multe linii epipolare din ambele imagini reprezintă, de asemenea, mănunchiuri de linii drepte care se intersectează la e 1Și e 2 .

Puncte m 1Și m 2 se numesc corespunzatoare daca sunt proiectii ale aceluiasi punct scena M. Liniile epipolare l 1Și l 2 se numesc corespunzatoare daca se afla in acelasi plan epipolar P. Daca planul epipolar P trece printr-un punct m 1, apoi liniile epipolare l 1Și l 2, aflate în el se numesc corespunzător punctului m 1.

Restricții privind poziția punctelor corespunzătoare m 1Și m 2, care rezultă din geometria epipolară, poate fi formulată astfel: punct m 2, corespunzătoare m 1, trebuie să se afle pe linia epipolară l 2, corespunzătoare m 1. Această condiție se numește constrângere epipolară. În coordonate omogene, condiția ca un punct m se află pe linie l scris ca l T m=0. Linia epipolară trece și prin punctul epipolar. Ecuația unei drepte care trece prin puncte m 1Și e 1 poate fi scris ca:

l 1 ∼ x m 1,

Unde X- o matrice antisimetrică de dimensiunea 3*3 astfel încât, x m 1- produs vectorial m 1Și e 1.

Pentru liniile epipolare corespunzătoare l 1Și l 2 dreapta:

Unde P+- pseudoinversie a matricei P.

Matricea F se numește matrice fundamentală. Este un operator liniar care asociază fiecare punct m 1 linia epipolară corespunzătoare l 2. Pentru fiecare pereche de puncte corespunzătoare m 1Și m 2 dreapta

m T 2 Fm 1 =0

Aceasta este o formulare a constrângerii epipolare prin matricea fundamentală.

Matricea fundamentală are 7 grade de libertate. Fiecare pereche de puncte corespunzătoare m 1Și m 2 definește o ecuație liniară pentru elementele matricei, deci poate fi calculată din cele 7 perechi cunoscute de puncte corespunzătoare.

Constrângerea epipolară este valabilă pentru orice perechi de puncte corespunzătoare situate pe planuri ideale de două tipuri. Dacă se cunosc matricele de calibrare internă K 1Și K2 camere de ambele tipuri, atunci constrângerea epipolară pentru punctele corespunzătoare din planurile ideale este scrisă astfel:

Se numește matricea E semnificativ matrice. Se poate arăta că matricea esențială poate fi obținută și din pozițiile relative ale camerelor.

Lăsa P 1 =(I|0)Și P2 =(R|-RT)- două matrice de proiectare cu calibrare K = I. Apoi ecuațiile de proiectare pentru planul ideal al ambelor camere se scriu sub forma:

Să găsim linia epipolară în a doua vedere corespunzătoare punctului m" 1 la primul. Pentru a face acest lucru, este suficient să proiectați pe a doua vedere două puncte situate pe rază (C 1 ,m" 1) la a doua vedere, de exemplu centrul primei camere (0,0,0,1) Tși un punct pe planul infinitului (x" 1 ,y" 1 ,z" 1 ,0) T. Proiecțiile acestor puncte vor fi -RT și R(x" 1 ,y" 1 ,z" 1 ,0) T. Ecuația liniei epipolare l 2, trecerea prin ambele puncte este dată ca produs vectorial:

l 2 =RT×R(x" 1 ,y" 1 ,z" 1) T =R(T×(x" 1 ,y" 1 ,z" 1) T)

Sub formă de matrice, un vector nu este un produs T×(x" 1 ,y" 1 ,z" 1) T poate fi scris folosind matricea S:

Atunci constrângerea epipolară asupra punctelor din planul ideal se scrie astfel:

Exprimarea matricei esențiale în ceea ce privește parametrii externi de calibrare a celor două camere este utilizată pentru a calcula pozițiile relative ale camerelor.

Proprietăți geometrice ale a trei sau mai multe imagini

Lăsa C 1,C 2Și C 3- centrele a trei vederi ale aceleiași scene tridimensionale. În acest caz, constrângerile epipolare sunt impuse punctelor corespunzătoare ale oricărei perechi de specii. Dacă se cunosc proiecţiile a două puncte m 1Și m 2 la prima și a doua vedere, apoi poziția proiecției la a treia imagine poate fi găsită ca intersecția a două vederi epipolare corespunzătoare punctelor m 1Și m 2.

Conform a două proiecții cunoscute m 1Și m 2 Folosind două imagini cu o calibrare cunoscută, se poate determina poziția punctului M în spațiu. Prin urmare, dacă calibrarea celei de-a treia imagini este cunoscută, atunci proiecția punctului M pe a treia vedere poate fi determinată printr-o proiecție simplă.

Constrângerile impuse asupra poziției punctelor corespunzătoare din mai mult de două imagini pot fi de asemenea scrise formă liniară. Pentru trei tipuri, aceste restricții sunt scrise sub forma unui tensor trifocal, pentru patru tipuri - sub forma unui tensor cvadrifocal. Cu toate acestea, calcularea acestor constrângeri este echivalentă cu calcularea gabaritului tuturor celor trei sau patru vederi în spațiul proiectiv. Aceste tipuri de restricții nu sunt utilizate în această lucrare și, prin urmare, nu sunt discutate mai detaliat.

La un moment dat, orice dezvoltator din domeniul graficii pe computer are o întrebare: cum funcționează aceste matrici promițătoare? Uneori, răspunsul este foarte greu de găsit și, așa cum se întâmplă de obicei, majoritatea dezvoltatorilor renunță la jumătatea sarcinii.

Aceasta nu este o soluție la problemă! Să ne dăm seama împreună!

Să fim realiști cu o părtinire practică și să luăm OpenGL versiunea 3.3 ca subiect de testare. Începând de la această versiune, fiecare dezvoltator este obligat să implementeze independent modulul de operații cu matrice. Grozav, de asta avem nevoie. Să ne descompunem sarcina dificilă și să evidențiem punctele principale. Câteva fapte din specificația OpenGL:

  • Matricele sunt stocate în coloane (coloană-major);
  • Coordonate omogene;
  • Volum de tăiere canonic (CVV) într-un sistem de coordonate pentru stânga.
Există două moduri de a stoca matrice: coloană-major și rând-major. În cursurile de algebră liniară se folosește schema de rânduri majore. În general, reprezentarea matricelor în memorie nu contează, deoarece o matrice poate fi întotdeauna convertită de la un tip de reprezentare la altul prin simplă transpunere. Și, deoarece nu există nicio diferență, atunci pentru toate calculele ulterioare vom folosi matrice clasice de rânduri majore. Când programați OpenGL, există un mic truc care vă permite să evitați transpunerea matricelor, menținând în același timp calculele clasice de rânduri majore. Matricea trebuie transferată în programul shader așa cum este, iar în shader multiplicarea trebuie efectuată nu între un vector și o matrice, ci între o matrice și un vector.

Coordonatele omogene nu sunt un sistem foarte complicat cu o serie de reguli simple pentru transformarea coordonatelor carteziene familiare în coordonate omogene și invers. O coordonată omogenă este o matrice de rând de dimensiune. Pentru a converti o coordonată carteziană într-o coordonată omogenă, este necesar X, yȘi zînmulțiți cu orice număr real w(cu excepția lui 0). Apoi, trebuie să scrieți rezultatul în primele trei componente, iar ultima componentă va fi egală cu multiplicatorul w. Cu alte cuvinte:
- coordonate carteziene
w– număr real nu este egal cu 0

- coordonate omogene

Un mic truc: Dacă w este egal cu unu, atunci tot ceea ce este necesar pentru traducere este transferul componentelor X, yȘi zși atribuiți unul ultimei componente. Adică, obțineți o matrice de rând:

Câteva cuvinte despre calitate zero w. Din punctul de vedere al coordonatelor omogene, acest lucru este destul de acceptabil. Coordonatele omogene vă permit să faceți distincția între puncte și vectori. Într-un sistem de coordonate carteziene, o astfel de împărțire este imposibilă.

- punctul în care ( x, y, z) – Coordonate carteziene

- vector, unde ( x, y, z) – vector rază

Translația inversă a unui vârf din coordonatele omogene în coordonatele carteziene se realizează după cum urmează. Toate componentele unei matrice de rânduri trebuie împărțite la ultima componentă. Cu alte cuvinte:

- coordonate omogene
- coordonate carteziene

Principalul lucru pe care trebuie să-l știți este că toți algoritmii de tăiere și rasterizare OpenGL funcționează în coordonate carteziene, dar înainte de asta toate transformările sunt efectuate în coordonate omogene. Trecerea de la coordonatele omogene la coordonatele carteziene se realizează în hardware.

Volumul canonic de tăiere (CVV) este una dintre părțile cel mai puțin documentate ale OpenGL. După cum se poate observa din fig. 1 CVV este un cub aliniat pe axă centrat la origine și cu o lungime a muchiei egală cu două. Tot ceea ce se încadrează în zona CVV este supus rasterizării, tot ceea ce este în afara CVV este ignorat. Orice lucru care intră parțial în afara CVV este supus algoritmilor de tăiere. Cel mai important lucru pe care trebuie să-l știți este că sistemul de coordonate CVV este stângaci!


Orez. 1. Volum de tăiere canonic OpenGL (CVV)

Sistem de coordonate pentru stângaci? Cum poate fi acest lucru, deoarece specificația pentru OpenGL 1.0 afirmă clar că sistemul de coordonate folosit este dreptaci? Să ne dăm seama.


Orez. 2. Sisteme de coordonate

După cum se poate observa din fig. Cele 2 sisteme de coordonate diferă doar în direcția axei Z. OpenGL 1.0 folosește un sistem de coordonate pentru utilizator dreptaci. Dar sistemul de coordonate CVV și sistemul de coordonate utilizator sunt două lucruri complet diferite. În plus, începând cu versiunea 3.3, nu mai există un sistem de coordonate OpenGL standard. După cum am menționat mai devreme, programatorul însuși implementează modulul de operații cu matrice. Formarea matricelor de rotație, formarea matricelor de proiecție, căutarea unei matrici inverse, înmulțirea matricelor - acesta este setul minim de operații inclus în modulul operații matrice. Apar două întrebări logice. Dacă volumul de vizibilitate este un cub cu o lungime a muchiei egală cu două, atunci de ce este vizibilă pe ecran o scenă cu dimensiuni de câteva mii de unități? În ce moment se transformă sistemul de coordonate utilizator în sistemul de coordonate CVV? Matricele de proiecție sunt tocmai entitatea care se ocupă de aceste probleme.

Ideea principală a celor de mai sus este că dezvoltatorul însuși este liber să aleagă tipul de sistem de coordonate al utilizatorului și trebuie să descrie corect matricele de proiecție. Acest lucru completează faptele despre OpenGL și este timpul să punem totul împreună.

Una dintre cele mai comune și mai greu de înțeles matrice este matricea de transformare a perspectivei. Deci, cum se raportează la CVV și sistemul de coordonate al utilizatorului? De ce obiectele devin mai mici pe măsură ce distanța lor față de observator crește? Pentru a înțelege de ce obiectele se micșorează pe măsură ce distanța crește, să ne uităm la transformările matriceale ale unui model 3D pas cu pas. Nu este un secret pentru nimeni că orice model tridimensional constă dintr-o listă finită de vârfuri care suferă transformări de matrice complet independent unul de celălalt. Pentru a determina coordonatele unui vârf tridimensional pe un ecran de monitor bidimensional, trebuie să:

  1. Convertiți coordonatele carteziene în coordonate omogene;
  2. Înmulțiți coordonatele omogene cu matricea modelului;
  3. Rezultatul este înmulțit cu matricea de vizualizare;
  4. Înmulțiți rezultatul cu matricea de proiecție;
  5. Convertiți rezultatul din coordonate omogene în coordonate carteziene.
Conversia coordonatelor carteziene în coordonate omogene a fost discutată mai devreme. Sensul geometric al matricei modelului este de a transfera modelul de la un sistem de coordonate local la un sistem de coordonate global. Sau, după cum se spune, mutați vârfurile din spațiul model în spațiul mondial. Să spunem simplu, un obiect tridimensional încărcat dintr-un fișier este situat în spațiul model, unde coordonatele sunt măsurate în raport cu obiectul însuși. Apoi, folosind matricea modelului, modelul este poziționat, scalat și rotit. Ca rezultat, toate nodurile modelului 3D primesc coordonate omogene reale în scena 3D. Spațiul model în raport cu spațiul mondial este local. Din spațiul model, coordonatele sunt transferate în spațiul mondial (de la local la global). În acest scop, se utilizează o matrice model.

Acum să trecem la pasul trei. Aici intervine spațiul de vedere. În acest spațiu, coordonatele sunt măsurate în raport cu poziția și orientarea observatorului ca și cum el ar fi centrul lumii. Spațiul de vizualizare este local în raport cu spațiul mondial, deci coordonatele trebuie introduse în el (și nu scoase, ca în cazul precedent). Transformarea directă a matricei elimină coordonatele dintr-un anumit spațiu. Pentru a le introduce în ea, dimpotrivă, este necesară inversarea transformării matriceale, de aceea transformarea de tip este descrisă de matricea inversă. Cum se obține această matrice inversă? Mai întâi, să obținem matricea observatorului direct. Ce caracterizează un observator? Observatorul este descris de coordonatele în care se află și de vectorii direcției de vizualizare. Observatorul privește întotdeauna în direcția axei sale locale Z. Observatorul se poate deplasa în jurul scenei și se poate întoarce. În multe privințe, aceasta seamănă cu sensul matricei modelului. În mare, așa stau lucrurile. Cu toate acestea, pentru un observator, operația de scalare este lipsită de sens, prin urmare, un semn egal nu poate fi pus între matricea model a observatorului și matricea model a unui obiect tridimensional. Matricea model a observatorului este matricea directă dorită. Prin inversarea acestei matrice, obținem matricea de vedere. În practică, aceasta înseamnă că toate vârfurile din coordonatele omogene globale vor primi noi coordonate omogene în raport cu observatorul. În consecință, dacă observatorul a văzut un anumit vârf, atunci valoarea coordonatei omogene z a unui punct dat în spațiul de vizualizare va fi cu siguranță un număr pozitiv. Dacă vârful era în spatele observatorului, atunci valoarea coordonatei sale omogene zîn spațiul de vizualizare va fi cu siguranță un număr negativ.

Pasul patru este cel mai interesant pas. Pașii anteriori au fost discutați atât de detaliat în mod intenționat, astfel încât cititorul să aibă o imagine completă a tuturor operanzilor pasului al patrulea. La a patra etapă, coordonatele omogene sunt transferate din spațiul de vizualizare în spațiul CVV. Încă o dată, se subliniază faptul că toate vârfurile potențial vizibile vor avea o valoare pozitivă a coordonatei omogene. z.

Luați în considerare o matrice de forma:

Și un punct din spațiul omogen al observatorului:

Să înmulțim coordonata omogenă cu matricea în cauză:

Să convertim coordonatele omogene rezultate în coordonate carteziene:

Să presupunem că există două puncte în spațiul de vedere cu aceleași coordonate XȘi y, dar cu coordonate diferite z. Cu alte cuvinte, unul dintre puncte este în spatele celuilalt. Din cauza distorsiunii perspectivei, observatorul trebuie să vadă ambele puncte. Într-adevăr, reiese clar din formulă că datorită împărțirii prin coordonate z, compresia are loc la punctul de origine. Cu cât valoarea este mai mare z(cu cât punctul este mai departe de observator), cu atât compresia este mai puternică. Aceasta este explicația efectului de perspectivă.

Specificația OpenGL afirmă că operațiunile de tăiere și rasterizare sunt efectuate în coordonate carteziene, iar procesul de conversie a coordonatelor omogene în coordonate carteziene se realizează automat.

Matricea (1) este un șablon pentru o matrice de proiecție în perspectivă. După cum sa menționat mai devreme, sarcina matricei de proiecție constă din două puncte: stabilirea unui sistem de coordonate utilizator (stângaci sau dreptaci), transferarea volumului de vizibilitate al observatorului către CVV. Să derivăm o matrice de perspectivă pentru un sistem de coordonate de utilizator stângaci.

Matricea de proiecție poate fi descrisă folosind patru parametri (Fig. 3):

  • Unghiul de vizualizare în radiani ( fovy);
  • Raport de aspect ( aspect);
  • Distanța până la cel mai apropiat plan de tăiere ( n);
  • Distanța până la planul de tăiere îndepărtat ( f).


Orez. 3. Perspectivă volum de vizibilitate

Să luăm în considerare proiecția unui punct din spațiul observatorului pe marginea frontală a decupării volumului de vizibilitate în perspectivă. Pentru o mai mare claritate, în fig. 4 prezintă o vedere laterală. De asemenea, trebuie luat în considerare faptul că sistemul de coordonate utilizator coincide cu sistemul de coordonate CVV, adică sistemul de coordonate stânga este folosit peste tot.


Orez. 4. Proiectarea unui punct arbitrar

Pe baza proprietăților triunghiurilor similare, următoarele egalități sunt adevărate:

Să exprimăm yꞌ și xꞌ:

În principiu, expresiile (2) sunt suficiente pentru a obține coordonatele punctelor de proiecție. Cu toate acestea, pentru a ecraniza corect obiectele tridimensionale, trebuie să cunoașteți adâncimea fiecărui fragment. Cu alte cuvinte, este necesară stocarea valorii componentei z. Aceasta este valoarea folosită pentru testele de adâncime OpenGL. În fig. 3 este clar că valoarea zꞌ nu este potrivit ca adâncime a fragmentului, deoarece toate proiecțiile punctuale au aceeași valoare zꞌ. Calea de ieșire din această situație este folosirea așa-numitei pseudo-adâncimi.

Proprietăți de pseudoadâncime:

  1. Pseudo-adâncimea este calculată pe baza valorii z;
  2. Cu cât punctul este mai aproape de observator, cu atât pseudoadâncimea are mai puțină valoare;
  3. Toate punctele situate pe planul frontal al volumului de vizibilitate au o valoare pseudo-adâncime de -1;
  4. Toate punctele situate pe planul de tăiere îndepărtat al volumului de vizibilitate au o valoare pseudo-adâncime de 1;
  5. Toate fragmentele aflate în interiorul volumului de vizibilitate au o valoare pseudo-adâncime în intervalul [-1 1].
Să derivăm formula prin care se va calcula pseudo-adâncimea. Să luăm ca bază următoarea expresie:

Cote AȘi b trebuie calculat. Pentru a face acest lucru, folosim proprietățile pseudoadâncimii 3 și 4. Obținem un sistem de două ecuații cu două necunoscute:

Să adăugăm ambele părți ale sistemului și să înmulțim rezultatul cu produsul fn, în care fȘi n nu poate fi egal cu zero. Primim:

Să deschidem parantezele și să rearanjam termenii astfel încât doar partea cu A, iar în dreapta doar cu b:

Să înlocuim (6) în (5). Să transformăm expresia într-o fracție simplă:

Înmulțiți ambele părți cu -2fn, în care fȘi n nu poate fi egal cu zero. Să prezentăm altele asemănătoare, rearanjam termenii și exprimăm b:

Să substituim (7) în (6) și să exprimăm A:

În consecință componentele AȘi b sunt egale:

Acum să substituim coeficienții obținuți în matricea piesei de prelucrat (1) și să vedem ce se întâmplă cu coordonatele z pentru un punct arbitrar din spațiul omogen al observatorului. Înlocuirea se realizează după cum urmează:

Lăsați distanța până la planul frontal de tăiere n este egală cu 2 și distanța până la planul îndepărtat de tăiere f este egal cu 10. Luați în considerare cinci puncte din spațiul omogen al observatorului:

Poziția relativă a punctului și a volumului de vizibilitate
Punct Sens Descriere
1 1 Punctul este situat în fața planului de tăiere frontal al volumului de vizibilitate. Nu trece rasterizarea.
2 2 Punctul este situat pe marginea frontală a decupării volumului de vizibilitate. În curs de rasterizare.
3 5 Punctul este situat între marginea de tăiere frontală și marginea de tăiere îndepărtată a volumului de vizibilitate. În curs de rasterizare.
4 10 Punctul este situat pe marginea îndepărtată a limitei volumului vizibilității. În curs de rasterizare.
5 20 Punctul este situat dincolo de marginea îndepărtată a limitei de volum de vizibilitate. Nu trece rasterizarea.

Să înmulțim toate punctele cu matricea (8), apoi să convertim coordonatele omogene rezultate în coordonate carteziene . Pentru a face acest lucru, trebuie să calculăm valorile noilor componente omogene Și .
Punctul 1:

Rețineți că coordonatele omogene poziționat absolut corect în CVV și, cel mai important, testul de adâncime OpenGL este acum posibil, deoarece pseudo-adâncimea satisface pe deplin cerințele testului.

Cu coordonata z Ne-am dat seama, să trecem la coordonate XȘi y. După cum am menționat mai devreme, întregul volum de vizibilitate în perspectivă trebuie să se încadreze în CVV. Lungimea marginii CVV este de două. În consecință, înălțimea și lățimea volumului de vizibilitate în perspectivă trebuie să fie comprimate la două unități convenționale.

Avem la dispoziție un colț fovyși magnitudinea aspect. Să exprimăm înălțimea și lățimea folosind aceste valori.


Orez. 5. Volumul vizibilității

Din fig. 5 este clar că:

Acum putem obține vizualizarea finală a matricei de proiecție în perspectivă pentru un sistem de coordonate personalizat pentru stânga care lucrează cu CVV OpenGL:

Aceasta completează derivarea matricelor.

Câteva cuvinte despre DirectX - principalul concurent al OpenGL. DirectX diferă de OpenGL doar prin dimensiunile CVV-ului și poziționarea acestuia. În DirectX, CVV este un paralelipiped dreptunghic cu lungimi de-a lungul axelor sale XȘi y egal cu doi și de-a lungul axei z lungimea este egală cu unu. Gamă XȘi y este [-1 1], iar intervalul z egal cu . În ceea ce privește sistemul de coordonate CVV, DirectX, ca și OpenGL, utilizează un sistem de coordonate stângaci.

Pentru a afișa matrice de perspectivă pentru un sistem de coordonate personalizat pentru dreapta, trebuie să redesenați Fig. 2, Fig. 3 și Fig. 4 ținând cont de noua direcție a axei Z. Calculele ulterioare sunt complet similare, până la semn. Pentru matricele DirectX, proprietățile de pseudo-adâncime 3 și 4 sunt modificate pentru a se potrivi cu intervalul.

În acest moment, subiectul matricelor promițătoare poate fi considerat închis.