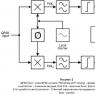
Metode de sortare. Quicksort este una dintre cele mai bune metode de sortare a tablourilor
Pentru a simplifica codul și a îmbunătăți lizibilitatea, vom introduce metoda Swap, care va schimba valorile din matrice după index.
Void Swap (T articole, int stânga, int dreapta) ( dacă (stânga != dreapta) (T temp = articole; articole = articole; articole = temp; ) )
Sortare cu bule
Sortarea cu bule este cel mai simplu algoritm de sortare. Se trece prin matrice de mai multe ori, la fiecare pas mutând cea mai mare valoare nesortată la sfârșitul matricei.
De exemplu, avem o matrice de numere întregi:
Prima dată când trecem prin matrice, comparăm valorile 3 și 7. Deoarece 7 este mai mare decât 3, le lăsăm așa cum sunt. Apoi comparăm 7 și 4. 4 este mai mic decât 7, așa că le schimbăm, deplasând pozițiile șapte cu o mai aproape de sfârșitul matricei. Acum arata cam asa:


Acest proces se repetă până când cei șapte ajung aproape la sfârșitul matricei. La sfârșit, este comparat cu elementul 8, care este mai mare, ceea ce înseamnă că nu are loc niciun schimb. După ce am parcurs o dată matricea, arată astfel:
Deoarece a fost făcut cel puțin un schimb de valoare, trebuie să trecem din nou prin matrice. Ca rezultat al acestei treceri, mutăm numărul 6 la loc.
Și din nou, a fost făcut cel puțin un schimb, ceea ce înseamnă că trecem din nou prin matrice.
La următoarea trecere, nu se face niciun schimb, ceea ce înseamnă că matricea noastră este sortată și algoritmul și-a terminat munca.
Public void Sortare(T articole) ( bool schimbat; do ( schimbat = fals; for (int i = 1; i< items.Length; i++) { if (items.CompareTo(items[i]) >0) ( Schimbat(articole, i - 1, i); schimbat = adevărat; ) ) ) în timp ce (schimbat != fals); )
Sortare prin inserare
Sortarea prin inserare funcționează prin iterarea unei matrice și mutarea valorii dorite la începutul matricei. După ce următoarea poziție este procesată, știm că toate pozițiile dinaintea ei sunt sortate, dar după ea nu sunt.
Un punct important: sortarea prin inserare procesează elementele matricei în ordine. Deoarece algoritmul iterează prin elemente de la stânga la dreapta, știm că totul din stânga indexului curent este deja sortat. Această figură arată cum crește porțiunea sortată a matricei cu fiecare trecere:


Treptat, partea sortată a matricei crește și, în cele din urmă, matricea va fi ordonată.
Să ne uităm la un exemplu concret. Iată matricea noastră nesortată pe care o vom folosi:


Algoritmul începe de la indexul 0 și valoarea 3. Deoarece acesta este primul index, matricea până la și inclusiv este considerată sortată.
În această etapă sunt sortate elementele cu indici 0..1, dar nu se știe nimic despre elementele cu indici 2..n.
Valoarea 4 este bifată în continuare, deoarece este mai mică de șapte, trebuie să o mutam în poziția corectă în partea sortată a matricei. Rămâne întrebarea: cum se definește? Acest lucru se face prin metoda FindInsertionIndex. Compară valoarea (4) care i-a fost transmisă cu fiecare valoare din partea sortată până când găsește un loc de inserat.
Deci, am găsit indicele 1 (între valorile 3 și 7). Metoda Insert realizează o inserare eliminând valoarea inserată din matrice și deplasând toate valorile, începând cu indexul de inserare, spre dreapta. Acum matricea arată astfel:


Acum este sortată partea matricei, care începe de la elementul zero și se termină cu elementul cu indicele 2. Următoarea trecere începe la indicele 3 și valoarea 4. Pe măsură ce algoritmul funcționează, continuăm să facem astfel de inserții.


Când nu mai sunt inserții disponibile, matricea este considerată complet sortată și algoritmul este terminat.
Public void Sortare(T articole) ( int sortedRangeEndIndex = 1; while (sortedRangeEndIndex)< items.Length) { if (items.CompareTo(items) < 0) { int insertIndex = FindInsertionIndex(items, items); Insert(items, insertIndex, sortedRangeEndIndex); } sortedRangeEndIndex++; } } private int FindInsertionIndex(T items, T valueToInsert) { for (int index = 0; index < items.Length; index++) { if (items.CompareTo(valueToInsert) >0) ( return index; ) ) throw new InvalidOperationException ("Indexul de inserare nu a fost găsit"); ) private void Insert(T itemArray, int indexInsertingAt, int indexInsertingFrom) ( // itemArray = 0 1 2 4 5 6 3 7 // insertingAt = 3 // insertingFrom = 6 // // Acțiuni: // 1: Salvați curentul index în temp // 2: Înlocuiți indexInsertingAt cu indexInsertingFrom // 3: Înlocuiți indexInsertingAt cu indexInsertingFrom la poziția +1 // Schimbați elementele la stânga cu unul // 4: Scrieți temp la poziția matricei + 1. // Pasul 1. T temp = itemArray; // Pasul 2. itemArray = itemArray; // Pasul 3. for (int current = indexInsertingFrom; curent > indexInsertingAt; curent--) ( itemArray = itemArray; ) // Pasul 4. itemArray = temp;
Sortare după selecție
Sortarea prin selecție este un hibrid între sortarea cu bule și sortarea prin inserție. La fel ca sortarea cu bule, acest algoritm trece prin matrice din nou și din nou, mutând o valoare în poziția corectă. Cu toate acestea, spre deosebire de sortarea cu bule, selectează cea mai mică valoare nesortată în loc de cea mai mare. Ca și în cazul sortării prin inserție, partea ordonată a matricei este situată la început, în timp ce în sortarea cu bule se află la sfârșit.
Să vedem cum funcționează sortarea prin selecție pe matricea noastră nesortată.


La prima trecere, algoritmul folosește metoda FindIndexOfSmallestFromIndex pentru a găsi cea mai mică valoare din matrice și pentru a o muta la început.
Cu o matrice atât de mică, putem spune imediat că cea mai mică valoare este 3 și este deja în poziția corectă. În acest moment știm că prima poziție din matrice (index 0) este cea mai mică valoare, prin urmare începutul matricei este deja sortat. Deci începem o a doua trecere - de data aceasta folosind indici de la 1 la n - 1.
La a doua trecere, determinăm că cea mai mică valoare este 4. O schimbăm cu al doilea element, șapte, după care 4 este plasat în poziția corectă.


Acum partea nesortată a matricei începe la indexul 2. Crește cu un element cu fiecare trecere a algoritmului. Dacă la orice trecere nu am făcut un singur schimb, aceasta înseamnă că matricea este sortată.
După încă două treceri, algoritmul își finalizează munca:


Public void Sortare(T articole) ( int sortedRangeEnd = 0; while (sortedRangeEnd)< items.Length) { int nextIndex = FindIndexOfSmallestFromIndex(items, sortedRangeEnd); Swap(items, sortedRangeEnd, nextIndex); sortedRangeEnd++; } } private int FindIndexOfSmallestFromIndex(T items, int sortedRangeEnd) { T currentSmallest = items; int currentSmallestIndex = sortedRangeEnd; for (int i = sortedRangeEnd + 1; i < items.Length; i++) { if (currentSmallest.CompareTo(items[i]) >0) ( currentSmallest = itemi[i]; currentSmallestIndex = i; ) ) return currentSmallestIndex; )
Sortare îmbinare
Împărțiți și guvernați
Până acum ne-am uitat la algoritmi liniari. Ei folosesc puțină memorie suplimentară, dar au complexitate pătratică. Folosind sortarea prin îmbinare ca exemplu, ne vom uita la un algoritm de împărțire și cucerire. (diviza și cuceri).
Acest tip de algoritm funcționează prin împărțirea unei probleme mari în altele mai mici, mai ușor de rezolvat. Le folosim în fiecare zi. De exemplu, căutarea în agenda telefonică este un exemplu de astfel de algoritm.
Dacă doriți să găsiți o persoană pe nume Petrov, nu veți căuta începând cu litera A și întorcând o pagină pe rând. Cel mai probabil vei deschide cartea undeva la mijloc. Dacă apăsați pe T, veți întoarce câteva pagini înapoi, poate prea multe la O. Apoi veți merge înainte. Astfel, răsfoind înainte și înapoi prin tot mai puține pagini, veți găsi în cele din urmă pe cea de care aveți nevoie.
Cât de eficienți sunt acești algoritmi?
Să presupunem că există 1000 de pagini în agenda telefonică. Dacă îl deschizi la jumătate, arunci 500 de pagini care nu conțin persoana pe care o cauți. Dacă nu ajungi la pagina din dreapta, selectezi partea dreaptă sau stângă și rămâi din nou cu jumătate din opțiunile disponibile. Acum aveți 250 de pagini pe care să vă uitați. În acest fel ne împărțim problema în jumătate din nou și din nou și putem găsi o persoană în agenda telefonică în doar 10 priviri. Aceasta reprezintă 1% din numărul total de pagini pe care ar trebui să le căutăm într-o căutare liniară.
Sortare îmbinare
În sortarea prin îmbinare, împărțim matricea în jumătate până când fiecare secțiune are o lungime de un element. Apoi, aceste secțiuni sunt returnate la locul lor (combinate) în ordinea corectă.
Să ne uităm la o matrice ca aceasta:
Să o împărțim în jumătate:
Și vom împărți fiecare parte în jumătate până când vor rămâne părți cu un element rămas:

Acum că am împărțit matricea în cele mai scurte secțiuni posibile, le îmbinăm în ordinea corectă.

Mai întâi obținem grupuri de două elemente sortate, apoi le „colectăm” în grupuri de patru elemente și, în final, colectăm totul într-o matrice sortată.

Pentru ca algoritmul să funcționeze, trebuie să implementăm următoarele operații:
- O operație pentru împărțirea recursiv a unui tablou în grupuri (metoda Sort).
- Fuzionarea în ordinea corectă (metoda Merge).
Este demn de remarcat faptul că, spre deosebire de algoritmii de sortare liniară, sortarea prin îmbinare va împărți și îmbina matricea, indiferent dacă a fost sortată inițial sau nu. Prin urmare, deși în cel mai rău caz va funcționa mai rapid decât liniar, în cel mai bun caz, performanța sa va fi mai mică decât cea liniară. Prin urmare, sortarea prin îmbinare nu este cea mai bună soluție atunci când trebuie să sortați o matrice parțial ordonată.
Public void Sortare (T articole) ( dacă (articole.Lungime<= 1) { return; } int leftSize = items.Length / 2; int rightSize = items.Length - leftSize; T left = new T; T right = new T; Array.Copy(items, 0, left, 0, leftSize); Array.Copy(items, leftSize, right, 0, rightSize); Sort(left); Sort(right); Merge(items, left, right); } private void Merge(T items, T left, T right) { int leftIndex = 0; int rightIndex = 0; int targetIndex = 0; int remaining = left.Length + right.Length; while(remaining >0) ( if (leftIndex >= left.Length) ( elemente = dreapta; ) else if (rightIndex >= right.Length) ( itemi = stânga; ) else if (left.CompareTo(right)< 0) { items = left; } else { items = right; } targetIndex++; remaining--; } }
Sortare rapida
Quicksort este un alt algoritm de împărțire și cucerire. Funcționează repetând recursiv următorii pași:
- Selectați un index cheie și împărțiți matricea în două părți folosindu-l. Acest lucru se poate face în diferite moduri, dar în acest articol folosim un număr aleatoriu.
- Mutați toate elementele mai mari decât cheia în partea dreaptă a matricei și toate elementele mai mici decât cheia în stânga. Elementul cheie este acum în poziția corectă - este mai mare decât orice element din stânga și mai mic decât orice element din dreapta.
- Repetăm primii doi pași până când matricea este complet sortată.
Să vedem cum funcționează algoritmul pe următoarea matrice:


Mai întâi selectăm aleatoriu un element cheie:
Int pivotIndex = _pivotRng.Next(stânga, dreapta);


Acum că știm indexul cheii (4), luăm valoarea situată la acel indice (6) și mutam valorile în matrice, astfel încât toate numerele mai mari sau egale cu cheia să fie în partea dreaptă și toate numerele mai mici decât cheia sunt în stânga . Rețineți că indexul elementului cheie se poate modifica în timpul procesului de transfer al valorilor (vom vedea acest lucru în curând).
Mutarea valorilor se face folosind metoda partiției.


În acest moment știm că valoarea 6 este în poziția corectă. Acum repetam acest proces pentru partea dreapta si stanga a matricei.
Rămânem cu o singură valoare nesortată și, din moment ce știm că totul a fost deja sortat, algoritmul se termină.
Random _pivotRng = new Random(); public void Sortare(T articole) ( sortare rapidă(articole, 0, articole.Lungime - 1); ) sortare rapidă private void(T articole, int stânga, int dreapta) ( if (stânga)< right) { int pivotIndex = _pivotRng.Next(left, right); int newPivot = partition(items, left, right, pivotIndex); quicksort(items, left, newPivot - 1); quicksort(items, newPivot + 1, right); } } private int partition(T items, int left, int right, int pivotIndex) { T pivotValue = items; Swap(items, pivotIndex, right); int storeIndex = left; for (int i = left; i < right; i++) { if (items[i].CompareTo(pivotValue) < 0) { Swap(items, i, storeIndex); storeIndex += 1; } } Swap(items, storeIndex, right); return storeIndex; }
Concluzie
Aceasta încheie seria noastră de articole despre algoritmi și structuri de date pentru începători. În acest timp, am acoperit liste legate, matrice dinamice, arbori binari de căutare și seturi cu exemple de cod în C#.
Acest articol discută algoritmi de sortare a matricei. Pentru început, algoritmii selectați pentru testare sunt prezentați cu o scurtă descriere a funcționării lor, după care se efectuează direct testarea, ale cărei rezultate sunt introduse într-un tabel și se trag concluziile finale.
Algoritmii de sortare sunt folosiți pe scară largă în programare, dar uneori programatorii nici măcar nu se gândesc la ce algoritm funcționează cel mai bine (termenul „cel mai bun” înseamnă o combinație de viteză și complexitate atât a scrierii, cât și a execuției).
În acest articol vom încerca să aflăm. Pentru a asigura cele mai bune rezultate, toți algoritmii prezentați vor sorta o matrice întregă de 200 de elemente. Calculatorul pe care se vor efectua testarea are următoarele caracteristici: procesor AMD A6-3400M 4x1.4 GHz, 8 GB RAM, sistem de operare Windows 10 x64 build 10586.36.
Pentru studiu au fost selectați următorii algoritmi de sortare:
Sortare selecție– esența algoritmului este de a parcurge matricea de la început până la sfârșit, găsind elementul minim al matricei și mutându-l la început. Complexitatea unui astfel de algoritm este O(n2).
Sortare cu bule– acest algoritm schimbă două elemente adiacente dacă primul element al matricei este mai mare decât al doilea. Aceasta continuă până când algoritmul schimbă toate elementele nesortate. Complexitatea acestui algoritm de sortare este O(n^2).
Sortare prin inserare– algoritmul sortează matricea pe măsură ce trece prin elementele sale. La fiecare iterație, un element este luat și comparat cu fiecare element din partea deja sortată a matricei, găsind astfel „locul său”, după care elementul este inserat în poziția sa. Acest lucru se întâmplă până când algoritmul trece prin întreaga matrice. Ieșirea este o matrice sortată. Complexitatea acestui algoritm este O(n^2).
Sortare rapida– esența algoritmului este împărțirea matricei în două sub-matrice, linia de mijloc este elementul care se află chiar în centrul matricei. În timpul funcționării algoritmului, elementele mai mici decât media vor fi mutate la stânga, iar cele mai mari la dreapta. Aceeași acțiune va avea loc recursiv cu sub-matrice, acestea vor fi împărțite în alte două sub-matrice până când nu mai este nimic de împărțit (un element rămâne). Ieșirea este o matrice sortată. Complexitatea algoritmului depinde de datele de intrare și în cel mai bun caz va fi egală cu O(n×2log2n). Cel mai rău caz O(n^2). Există, de asemenea, o medie, care este O(n×log2n).
Sortare pieptene– ideea cum funcționează algoritmul este extrem de similară cu sortarea de schimb, dar principala diferență este că nu sunt comparate două elemente adiacente, ci elemente dintr-un interval de, de exemplu, cinci elemente. Acest lucru asigură că valorile mici nu sunt aruncate la sfârșit, ceea ce ajută la accelerarea sortării pe matrice mari. Prima iterație este efectuată în incremente calculate prin formula (dimensiunea matricei)/(factor de reducere), unde factorul de reducere este de aproximativ 1,247330950103979 sau rotunjit la 1,3. A doua iterație și cele ulterioare vor continua cu pasul (pasul curent)/(factor de reducere) și vor continua până când pasul este egal cu unu. În aproape orice caz, complexitatea algoritmului este O(n×log2n).
Pentru a efectua testarea, vor fi efectuate 5 rulări ale fiecărui algoritm și va fi selectat cel mai bun timp. Cel mai bun timp și memorie utilizată vor fi introduse într-un tabel. Vom testa, de asemenea, viteza de sortare a tablourilor de 10, 50, 200 și 1000 de elemente pentru a determina pentru ce sarcini este destinat un anumit algoritm.
O matrice complet nesortată:
Matrice parțial sortată (jumătate dintre elemente sunt sortate):

Rezultate prezentate în grafice:


Ca urmare a cercetării și a datelor obținute, pentru sortarea unui tablou nesortat, cel mai optim dintre algoritmii prezentați pentru sortarea unui tablou este sortarea rapidă. În ciuda timpului mai lung de execuție, algoritmul consumă mai puțină memorie, ceea ce poate fi important în proiectele mari. Cu toate acestea, algoritmi precum selecția, schimbul și sortarea prin inserție pot fi mai potriviti pentru scopuri științifice, cum ar fi învățarea, unde cantități uriașe de date nu trebuie procesate. Cu o matrice sortată parțial, rezultatele nu sunt mult diferite, toți algoritmii de sortare arată cu aproximativ 2-3 milisecunde mai puțin. Cu toate acestea, atunci când sortați o matrice parțial sortată, sortarea rapidă este mult mai rapidă și consumă mai puțină memorie.
Obiectul sortării externe este un fișier. Dimensiunea fișierului este fundamental nelimitată, adică este posibil să nu încapă în RAM. Pentru acest tip de sortare, costurile suplimentare ale memoriei externe nu sunt strict standardizate, astfel încât fișierele auxiliare sunt utilizate în mod activ. Accesul la fișiere este strict secvenţial. Această cerință se datorează a două circumstanțe. În primul rând, metodele externe de sortare trebuie să fie operabile atunci când se stochează fișiere pe dispozitive cu acces secvenţial, cum ar fi benzile magnetice. În al doilea rând, atunci când se utilizează accesul direct, principalele costuri de timp sunt asociate cu poziționarea fișierelor, care este de dorit să fie eliminată.
Metodele de sortare externă se bazează pe procedura de îmbinare, care implică combinarea a două sau mai multe secvențe sortate. Să luăm în considerare această procedură folosind exemplul de îmbinare a două secvențe A și B în secvența C. Să fie sortate elementele A și B în ordine crescătoare, adică a 1 £ a 2 £ … £ a m și b 1 £ b 2 £ … £ b n . Se cere ca șirul C să fie aranjat și în ordine crescătoare, adică se satisface c 1 £ c 2 £ …£ c m + n.
În primul rând, primele elemente ale secvențelor sunt selectate ca fiind curente. Cel mai mic este scris în C, iar următorul element din aceeași secvență devine curent. Această operație se repetă până când una dintre secvențe este epuizată, după care restul celeilalte secvențe se adaugă la C.
Puteți observa că accesul la elementele A, B și C a fost efectuat strict secvenţial. În metodele de sortare externă, secțiunile sortate ale fișierelor apar ca secvențe A, B și C.
Metoda de bază de sortare externă este metoda simplă de îmbinare. Să ne uităm la asta folosind următorul exemplu. Să existe un fișier A care conține elementele 27, 16, 13, 11, 18, 25, 7. Acest fișier este împărțit în două fișiere B și C prin scrierea alternativă a elementelor în aceste fișiere. Să arătăm asta cu o diagramă
B: 27, 13, 18, 7
A: 27, 16, 13, 11, 18, 25, 7
Fișierele B și C sunt apoi unite din nou prin inserarea alternativă a elementelor din A și B în C, cu elementul mai mic al fiecărei perechi plasat primul. Veți obține următorul rezultat
B: 27, 13, 18, 7
Perechile sunt separate una de alta prin apostrofe. În etapa următoare, fișierul A este din nou împărțit în B și C, dar nu elemente individuale, dar perechile selectate sunt scrise pe rând în fiecare fișier. Primim
B: 16, 27, 18, 25
A: 16, 27, 11, 13, 18, 25, 7
B: 16, 27, 18, 25
A: 11, 13, 16, 27,’ 7, 18, 25
Fișierul A este apoi distribuit în cvadruple de elemente și, atunci când este reunit, va fi format din opturi ordonate de elemente. În exemplul nostru, sortarea se va încheia în această etapă. În general, lungimea seriei sortate va crește în puteri de 2 până când dimensiunea seriei depășește numărul de elemente din fișier.
Folosind acest exemplu, vom defini termenii de bază ai sortării externe. Metoda a implicat 3 fișiere, motiv pentru care se numește trei bandă. Au fost necesare 3 treceri pentru a finaliza sortarea. O singură trecere a constat din rutine de împărțire și îmbinare, fiecare procesând toate elementele. Astfel de proceduri se numesc faze. Prin urmare, metoda simplă de fuziune este în două faze și trei benzi.
Există o îmbunătățire evidentă a metodei. Rezultatul fuziunii este distribuit imediat în două benzi, adică 4 casete sunt deja implicate în proces. Datorită memoriei suplimentare, numărul de operații de rescriere este redus la jumătate. Aceasta este o metodă monofazată cu patru benzi, numită și fuziune echilibrată.
După cum se poate observa din datele de mai sus, metoda poate concura în viteză cu cele mai rapide metode de sortare internă, dar nu este utilizată ca atare, deoarece necesită costuri semnificative de memorie. Numărul de treceri este estimat prin log 2 n, iar numărul total de transferuri M este proporțional cu n log 2 n.
Metoda simplă de îmbinare nu oferă niciun beneficiu în cazurile în care fișierul A este sortat complet sau parțial. Acest dezavantaj nu este prezent în metoda fuziunii naturale.
Să numim o serie o succesiune de elemente a i, a i +1, …, a j, satisfăcând relațiile a i -1 > a i £ a i +1 £ …£ a j > a j +1. În cazuri speciale, o serie poate fi la începutul sau la sfârșitul unei secvențe.
Fișierul sursă A este împărțit în serii. Distribuția pentru B și C se realizează pe serii. Când sunt conectate, perechile de serie se îmbină. Din nou, sunt posibile atât o versiune cu trei benzi, cât și o versiune cu patru benzi a metodei. Mai jos este un exemplu de sortare naturală prin îmbinare cu 4 benzi.
B: 17, 25, 41, ‘6
A: 17, 25, 41, ' 9, 11, ' 6, ' 3, 5, 8, 44
C: 9, 11, '3, 5, 8, 44
A: 9, 11, 17, 25, 41 B: 3, 5, 6, 8, 9, 11, 17, 25, 41, 44
D: 3, 5, 6, 8, 44 C:
La ultima divizare, banda C este goală, iar fișierul sortat rămâne pe banda B.
Metoda de îmbinare naturală este în general mai rapidă, dar necesită mai multe comparații, deoarece necesită determinarea sfârșitului fiecărei rulări. Mai jos este un program pentru sortarea unui fișier folosind metoda de îmbinare naturală în două faze cu trei benzi.
Programul SortSlian;
(sortare naturală de îmbinare în 3 benzi, în 2 faze)
(cheile sunt întregi și pozitive)
Tastați elem=record
(alte domenii)
bandă = dosar de elem;
Nume: sfoară; (numele fișierului sursă)
Procedura Vvod(var F: bandă);
În timp ce K<>-1 fac
Write("Introduceți următoarea cheie (sfârșitul -1): ");
dacă K<>-1 apoi scrieți (F, S)
Procedura Pech(var F: bandă);
Deși nu eof(F) face
Scrie(S. Key," ")
Procedură CopyElem(var X, Y: bandă;
var Buf: elem; var E: boolean);
(copierea unui element și citirea următorului
(în Buf cu verificarea sfârșitului de serie (E=True))
dacă nu Eof(X), atunci Read(X, Buf)
else Buf.Key:=-1; (barieră: sfârșitul fișierului atins)
E:=(Buf.Key Procedură CopySer(var X, Y: bandă; var Buf: elem); (copierea unei serii de la X la Y) (la începutul lui Buf este primul element al seriei curente pe X) (final Buf - primul element al următorului sau -1 (sfârșitul X) ) dacă Buf.Key>0 atunci (fișierul X nu este citit) CopyElem(X, Y, Buf, E) Până la E (E=Adevărat la sfârșitul seriei) Distribuirea procedurii; (distribuția A --> B și C) Citiți(A, S); (primul element al lui A) Rescrie(B); Rescrie (C); CopySer(A, B, S); (S este primul element al seriei următoare) dacă S.Key>0 atunci (fișierul A nu este copiat complet) CopySer(A, C, S) Până la S.Key<0 Procedura Slian; (combinarea dintre B și C--->A) E1, E2: boolean; Procedura SlianSer; (combinarea seriilor din B și C ---> A) (S și T sunt primele elemente ale seriei) (S.Cheie<0-весь файл B считан, T.Key<0-файл C считан } E1:=fals; E2:=fals; dacă (S.Key>0) și ((S.Key (fișierul B nu a fost citit și elementul curent al lui B este mai mic decât în C sau fișierul C a fost citit complet) CopyElem(B, A, S, E1); dacă E1 atunci (a ajuns la sfârșitul seriei pe B) CopyServ (C, A, T) CopyElem(C, A, T, E2); dacă E2 atunci (s-a ajuns la sfârșitul seriei pe C) CopySer(B, A, S) Începutul (începutul lui Slian) dacă nu (Eof(B) sau Eof(C)) atunci începe (ambele fișiere nu sunt goale) L:=0; (contor de episoade) În timp ce (S.Key>0) sau (T.Key>0) fac Început (începutul programului principal) Write("Introduceți un nume de fișier pentru a scrie articole: "); Atribuie(A, Nume); Atribuie(B, "Rab1"); Atribuie(C, "Rab2"); L:=0; (L - numărul de serii după îmbinare - parametru) WriteLn("Fișier A: "); Pech(A); Raspred; (faza de distribuție) WriteLn("Fișier B: "); Pech(B); WriteLn("Fișier C: "); Pech(C); ReadLn; (pauză) Slian (faza de fuziune) Până la L<=1; { L=0, если исходный файл отсортирован } WriteLn("Fișierul A la sfârșit: "); Închidere(B); Șterge (B); (Ștergerea fișierelor de lucru) Închidere(C); Șterge (C); Merită să acordați atenție procedurii de copiere a unui element din bandă în bandă CopyElem. În realitate, un element din RAM rămas din copia anterioară este scris în fișier, iar următorul element al acestui fișier este citit în memorie. Acest lucru se datorează nevoii de a verifica constant sfârșitul seriei. Trebuie să ținem cont în special de cazul în care sfârșitul seriei coincide cu sfârșitul dosarului. La îmbinare, se numără numărul de serii rezultate. Sortarea se termină când rămâne o singură serie. Eficiența sortării poate fi îmbunătățită prin utilizarea îmbinării cu mai multe căi, în care distribuția este efectuată pe k benzi. Deoarece numărul de serii la fiecare trecere scade cu un factor k, numărul de transferuri M este proporțional cu n log k n. Dacă numărul total de benzi este par, atunci se poate folosi metoda de îmbinare monofazată, distribuind serii de la o jumătate a benzilor la cealaltă. Prețul pentru creșterea eficienței îmbinării cu mai multe căi este, ca întotdeauna, o creștere a complexității implementării și costuri suplimentare de memorie externă. Cât de diferit ar putea fi numărul de episoade după despărțire? La prima vedere pare că nu există mai mult de unul, dar nu este așa. De exemplu, atunci când se distribuie seria 17, 25, 41, ' 9, 60, ' 50, 52, ' 7, prima și a treia serie se îmbină într-o serie comună, ceea ce nu se întâmplă cu seria a doua și a patra. Drept urmare, în timpul unei fuziuni ulterioare, seria de pe una dintre benzi se poate termina mai devreme și va trebui să irosești restul celeilalte casete, pierzând eficiența. Astfel de situații sunt luate în considerare în metoda de sortare multifazică. Să ne uităm la el folosind trei benzi ca exemplu. Să presupunem că atunci când conectați benzile B și C la banda A, seria de pe B se termină mai devreme. Apoi banda B este declarată ieșire, iar banda A devine intrare. Procesul continuă până când situația se repetă din nou, când se termină seria de pe una dintre benzile de intrare. Sortarea în mai multe faze este posibilă și cu îmbinarea pe mai multe căi. De exemplu, dacă utilizați k benzi într-un sortare, puteți avea întotdeauna o bandă de ieșire. Când rulările pe una dintre benzile de intrare k-1 sunt epuizate, acea bandă devine banda de ieșire în loc de banda de ieșire anterioară. Metodele de sortare interne și externe pot fi utilizate împreună. Lasă un fișier mare să fie sortat. Un buffer de dimensiunea maximă posibilă este alocat în RAM. Fișierul este împărțit în blocuri corespunzătoare dimensiunii bufferului. Blocurile sunt citite într-un buffer, sortate folosind una dintre metodele interne de sortare și rescrise într-un alt fișier. Acum fiecare bloc al unui fișier nou este o serie de o lungime destul de mare, determinată de dimensiunea bufferului. Rămâne să se aplice una dintre metodele de sortare externă folosind datele de serie. Introducere
.
Au trecut aproximativ trei decenii și jumătate de când programarea computerelor a fost introdusă ca disciplină academică în universitățile pedagogice. Având în vedere viteza colosală a schimbărilor în subiectul în sine, care a depășit întotdeauna semnificativ viteza mecanismelor centrale de publicare, cărțile destinate în mod special programelor universităților pedagogice au fost publicate nu mai mult de o dată pe deceniu - aproape proporțional cu viteza de schimbare a generațiilor de calculatoare. . Astăzi, rafturile librăriilor sunt pline cu publicații despre informatică. Cu toate acestea, profesorul (și mai ales elevul) încă mai are nevoie de cărți educaționale speciale, al căror conținut și focalizare corespund programului și programului dat. Acum, pe lângă programare, în unele specialități, universitățile pedagogice au introdus și alte cursuri speciale mai complexe la intersecția dintre matematica aplicată (discretă) și informatica. În acest curs, vă puteți familiariza cu matricele și puteți afla despre metode simple și complexe de sortare a acestora, precum și care dintre ele sunt cele mai eficiente și în ce cazuri. Obiectivul principal este de a demonstra diferite metode de sortare și de a le evidenția pe cele mai eficiente. Sortarea este un exemplu destul de bun de problemă care poate fi rezolvată folosind mulți algoritmi diferiți. Fiecare dintre ele are propriile avantaje și dezavantaje și trebuie să alegeți un algoritm bazat pe formularea specifică a problemei. În general, sortarea ar trebui înțeleasă ca procesul de regrupare a unui set dat de obiecte într-o anumită ordine. Scopul sortării este de a facilita căutarea ulterioară a elementelor dintr-un astfel de set sortat. Aceasta este o activitate aproape universală, fundamentală. Întâlnim obiecte sortate în cărțile telefonice, în listele cu impozitul pe venit, în cuprinsul cărților, în biblioteci, în dicționare, în depozite - aproape oriunde trebuie să căutăm obiecte depozitate. Astfel, vorbirea despre sortare este destul de potrivită și importantă atunci când vine vorba de prelucrarea datelor. Interesul inițial pentru sortare se bazează pe faptul că atunci când construim algoritmi întâlnim multe tehnici foarte fundamentale. Aproape că nu există metode care să nu fie întâlnite atunci când discutăm această problemă. În special, sortarea este un subiect ideal pentru demonstrarea varietății uriașe de algoritmi, toți inventați pentru aceeași sarcină, mulți dintre ei optimi într-un anumit sens, majoritatea având propriile merite. Prin urmare, este și un obiect ideal pentru a demonstra necesitatea analizei performanței algoritmilor. În plus, folosind exemple de sortare, se poate arăta cum, complicând algoritmul, deși există deja metode evidente la îndemână, se poate obține un câștig semnificativ în eficiență. Alegerea algoritmului depinde de structura datelor care sunt procesate - aceasta este aproape o lege, dar în cazul sortării, această dependență este atât de profundă încât metodele corespunzătoare sunt împărțite în două clase - matrice de sortare și fișiere de sortare (secvențe). . Acestea sunt uneori numite sortări interne și externe, deoarece matricele sunt stocate în memoria internă rapidă, cu acces aleator, a mașinii, în timp ce fișierele sunt de obicei localizate în memorie externă mai lentă, dar mai mare, dispozitive bazate pe mecanice (discuri sau benzi). Înainte de a merge mai departe, să introducem câteva concepte și notații. Dacă avem elemente a, a, …… , a atunci sortarea este rearanjarea acestor elemente într-o matrice k, ak, …… , ak unde ak ak ak . Presupunem că tipul de element este definit caÎNTREG. Constn =???; //lungimea necesară a matricei este indicată aici Var A: matrice de întreg; Selectați INTEGER într-o oarecare măsură arbitrară. S-a putut lua un alt tip pe care se defineşte relaţia de ordine generală. Se spune că o metodă de sortare este stabilă dacă poziția relativă a elementelor cu chei egale nu se modifică în timpul procesului de sortare. Stabilitatea sortării este adesea de dorit atunci când aveți de-a face cu elemente care sunt deja ordonate (sortate) după o cheie secundară (adică, proprietăți) care nu afectează cheia primară. Condiția principală: metoda aleasă de sortare a matricei trebuie să utilizeze cu moderație memoria disponibilă. Aceasta presupune că permutările care aduc elementele în ordine trebuie efectuate în același loc, adică metode în care elementele din tabloul a sunt trecute în tabloul rezultat b , prezintă un interes semnificativ mai mic. Vom clasifica mai întâi metodele în funcție de eficiența lor, adică în funcție de timpul lor de funcționare. O bună măsură a eficacității ar putea fi C – numărul de comparații cheie necesare și M – numărul de transferuri (permutări) elemente. Aceste numere sunt funcții ale n – numărul de elemente sortate. Deși algoritmii buni de sortare necesită ordine n* autentificare comparații, ne vom uita mai întâi la câteva metode simple și evidente, ele se numesc directe, unde este necesar ordinul de mărime n 2 comparații cheie. Următoarele motive ne obligă să începem analiza cu metode directe, fără a atinge algoritmi rapizi: Metodele directe sunt utile în special pentru explicarea trăsăturilor caracteristice ale principiilor de bază ale majorității soiurilor. Programele acestor metode sunt ușor de înțeles și scurte. Metodele complexe necesită un număr mare de operații și, prin urmare, pentru destul de mici n metodele directe sunt mai rapide, deși pentru mari n Desigur, ele nu ar trebui folosite. Metodele de sortare în același loc pot fi împărțite în trei categorii principale în funcție de principiile lor directoare: Sortați după includere ( prin inserare). Sortare folosind selecția ( prin selecție). Sortare folosind schimburi ( prin schimb). Vom explora acum aceste principii și le vom compara. Toate programele operează pe matricea a. Constn= a: matrice de numere întregi; Această metodă este utilizată pe scară largă atunci când se joacă cărți. Elementele sunt împărțite mental într-o secvență deja „gata” și, … , A și secvența originală. La fiecare pas, începând de la I = 2 și crescând i de fiecare dată câte unul, este extras din secvența originală i - al treilea element și este transferat în secvența terminată și este introdus în locul potrivit. PROGRAMUL 2.1. SORTARE CU PUTEREA DIRECTĂ. I,J,N,X:INTEGER; A:RAY OF INTEGER; SCRIE ("Introduceți lungimea matricei"); CITEȘTE(N); WRITELN('Introduceți matricea'); FOR I:=1 TO N DO READ(A[I]); PENTRU I:=2 TO N DO WRITELN("Rezultat:"); SFÂRŞIT. Acesta este un caz tipic al unui proces repetat cu două condiții terminațiile ne permite să folosim tehnica binecunoscută „barieră” (santinelă). Analiza metodei includerii directe. Numărul de comparații cheie ( Ci) pentru i - m cernere este cel mult egală cu i -1, cel puțin 1; dacă presupunem că toate permutările din n cheile sunt la fel de probabile, atunci numărul mediu de comparații este eu /2. Numărul de transferuri Mi este egal cu Ci + 2 (inclusiv bariera). Prin urmare, numărul total de comparații și numărul de transferuri sunt după cum urmează: Cmin = n-1 (2,1.) Mmin = 3*(n-1) (2,4.) Peștera = (n2+n-2)/4 (2.2.) Mave = (n2+9*n-10)/4 (2.5.) Cmax = (n2+n-4)/4 (2.3.) Mmax = (n2+3* n-4)/2 (2.6.) Algoritmul cu incluziuni directe poate fi îmbunătățit cu ușurință dacă acordați atenție faptului că secvența finală în care trebuie să introduceți un nou element este deja ordonată. Este firesc să se stabilească căutarea binară, în care se încearcă compararea cu mijlocul secvenței terminate, iar apoi procesul de înjumătățire continuă până când este găsit punctul de includere. Acest algoritm de sortare modificat se numește metoda de includere binară ( inserare binară). PROGRAMUL 2.2. METODĂ DE SORTARE ÎN JUMĂTĂTARE. I,J,M,L,R,X,N:INTEGER; A:RAY OF INTEGER; WRITELN("Introduceți matricea"); FOR I:=1 TO N DO READ(A[I]); PENTRU I:=2 TO N DO X:=A[I];L:=1;R:=I; FOR J:=I DOWNTO R+1 DO A[J]:=A; WRITELN("Rezultat:"); FOR I:=1 TO N DO SCRIE(A[I]," ") SFÂRŞIT. Analiza incluziunii binare. Punctul de includere este detectat dacă L=R . Astfel, la finalul căutării, intervalul trebuie să fie de unitate de lungime; asta înseamnă că este împărțit în jumătate I*logI o singura data. Prin urmare: C = Si: 1i n: [logI] (2.7.) Să aproximăm această sumă prin integrală Integrală (1:n) log x dx = n*(log n – C) + C (2.8.) Unde C = loge = 1/ ln 2 = 1,4426… . (2.9.) Această tehnică se bazează pe următoarele principii: Este selectat elementul cu cea mai mică cheie Schimbă locurile cu primul element a1. Acest proces se repetă apoi cu restul n-1 elemente, n -2 elemente etc. până la unu, cel mai mare element rămâne. PROGRAMUL 2.3. SORTARE CU SELECTARE DIRECTA. I,J,R,X,N:INTEGER; A:RAY OF INTEGER; WRITELN("Introduceți lungimea matricei"); WRITELN("Introduceți matricea"); FOR I:=1 TO N DO READ(A[I]); PENTRU I:=1 LA N-1 DO FOR J:=I+1 TO N DOIF A[J] WRITELN("Rezultat:"); FOR I:=1 TO N DO SCRIE(A[I]," ") SFÂRŞIT. Analiza selectiei directe. Numărul de comparații de chei (C) evident nu depinde de ordinea inițială a tastelor. Pentru C avem C = (n2 – n)/2 (2.10.). Numărul de permutări este minim: Mmin = 3*(n-1) (2,11). In cazul cheilor comandate initial si maxim Mmax = n2/4 + 3*(n-1) (2.12.) Să definim M avg . Pentru suficient de mare n putem ignora componentele fracționale și, prin urmare, putem aproxima numărul mediu de atribuiri prin i -a-a expresie de vizualizare Fi = lni + g + 1 (2.13.), unde g = 0,577216… - constanta lui Euler. Numărul mediu de transferuri Mavg în sortarea selecției există o sumă Fi cu i de la 1 la n Mavg = n*(g + 1) + (Si: 1 Din nou aproximând această sumă de termeni discreti prin integrală Integrală (1:n) ln x dx = x*(ln x – 1) = n*ln (n) – n + 1 (2.15.) Obținem o valoare aproximativă Mavg = n*(ln (n) + g) . (2.16.) 2.1.3. Sortare prin schimb direct
.
Ca și în metoda de selecție directă, repetăm trecerile prin matrice, de fiecare dată mutând cel mai mic element din secvența rămasă la capătul din stânga matricei. Dacă luăm în considerare formațiunile verticale mai degrabă decât orizontale, elementele pot fi interpretate ca bule într-o cuvă de apă, greutatea fiecăruia corespunzând cheii sale. PROGRAMUL 2.4. SORTAREA BULELOR. PROGRAME; I,J,X,N:INTEGER; A:RAY OF INTEGER; WRITELN("Introduceți lungimea matricei"); WRITELN("Introduceți matricea"); FOR I:=1 TO N DO READ(A[I]); PENTRU I:=2 TO N DO PENTRU J:=N JOS I DO DACA A>A[J] ATUNCI WRITELN("Rezultat:"); PENTRU I:=1 TO N DO SFÂRŞIT. Îmbunătățirile aduse acestui algoritm sugerează ele însele: Amintiți-vă dacă au existat sau nu rearanjamente în proces ceva pasaj. Amintiți-vă nu numai faptul că schimbul a avut loc, ci și poziţia (indicele) ultimului schimb. Alternează direcția vizualizărilor succesive. Vom numi algoritmul rezultat sortare „shaker” ( ShakerSoft). Analiza sortării cu bule și agitare. Numărul de comparații într-un algoritm strict de schimb C = (n2 – n )/2, (2.17.), și, respectiv, numărul minim, mediu și maxim de mișcări ale elementelor (atribuții) sunt M = 0, Mavg = 3*(n2 – n)/2, Mmax = 3*(n2 – n)/4 (2.18.) Analiza metodelor îmbunătățite, în special sortarea agitatorului, este destul de complexă. Număr minim de comparații Cmin = n – 1. Knuth consideră că numărul mediu de treceri de sortare îmbunătățită a bulelor este proporțional cu n – k1 n 1/2, iar numărul mediu de comparații este proporțional cu ½( n2 – n(k2 + lnn)). PROGRAMUL 2.5. SORTAREA SHAKER. PROGRAME; J,L,K,R,X,N,I:INTEGER; A:RAY OF INTEGER; WRITELN("Introduceți lungimea matricei'); WRITELN("Introduceți matricea"); PENTRU I:=1 TO N DO FOR J:=R DOWNTO L DO DACA A>A[J] ATUNCI PENTRU J:=L LA R DO DACA A>A[J] ATUNCI WRITELN("Rezultat:"); PENTRU I:=1 TO N DO SFÂRŞIT. De fapt, nu există nimic valoros în sortarea cu bule, în afară de numele său atractiv. Sortarea shaker este utilizată pe scară largă în cazurile în care se știe că elementele sunt aproape ordonate - în practică acest lucru este foarte rar. În 1959, D. Schell a propus o îmbunătățire a sortării folosind includerea directă. În primul rând, elementele separate de o distanță de 4 sunt sortate și grupate separat. Acest proces se numește sortare cvadruplă. În exemplul nostru există opt elemente și fiecare grup este format din două elemente. După prima trecere, elementele sunt regrupate - acum fiecare element al grupului este la două poziții față de celălalt - și sortate din nou. Aceasta se numește sortare dublă. A treia abordare implică sortarea obișnuită sau unică. În fiecare etapă, fie sunt sortate relativ puține elemente, fie elementele sunt deja destul de bine ordonate și necesită relativ puține rearanjamente. PROGRAMUL 2.6. SORTARE COCHILE... PROGRAMSHELLS; H: ARRAY OF INTEGER = (15,7,3,1); I,J,K,S,X,N,M:INTEGER; A:ARRAY[-16..50] OF INTEGER; WRITELN("Introduceți lungimea matricei"); WRITELN("Introduceți matricea"); PENTRU I:=1 TO N DO PENTRU M:=1 LA T FAC PENTRU I:=K+1 LA N DO DACĂ S=0 atunci S:=-K; WRITELN("Rezultat:"); PENTRU I:=1 TO N DO Analiza sortării Shell. Nu știm care distanțe dau cele mai bune rezultate. Dar nu ar trebui să fie multiplicatori unul pe celălalt. Următoarea teoremă este adevărată: dacă k -secventa sortata i -sortează, apoi rămâne k -sortat. Knuth arată că are sens să folosești o secvență în care hk-1 = 3 hk + 1, ht = 1 și t = [ log2 n] – 1. (2.19.) 2.2.2.Sortarea folosind un arbore
.
Metoda de sortare prin selecție directă se bazează pe căutări repetate pentru cea mai mică cheie dintre n elemente dintre n -1 elemente rămase etc. Cum putem îmbunătăți metoda de sortare menționată? Acest lucru se poate realiza urmând următorii pași de sortare: 1. Lăsați după fiecare trecere mai multe informații decât identificarea unui singur element minim. După ce a făcut n -1 comparații, putem construi un arbore de selecție ca cel prezentat în Figura 2.1. 44 12 18 06
44 55 12 42 94 18 06 67
FIGURA 2.1. SELECTARE REPETĂ DINTRE DOUĂ TASPE. 2. Coborârea pe traseul marcat de cel mai mic element și eliminarea acestuia din arbore prin înlocuirea acestuia fie cu un element gol în partea de jos, fie cu un element dintr-o ramură adiacentă la vârfurile intermediare (vezi Figurile 2.2 și 2.3.). D. Williams a inventat metoda Heapsort , în care s-a obținut o îmbunătățire semnificativă din sortarea tradițională pe bază de arbori. O piramidă este definită ca o secvență de taste a[ L], a[ L+1], … , a[ R], astfel încât a[ i] a și a[ i] a pentru i= L… R/2. R. Floyd a propus un anumit mod „laconic” de a construi o piramidă în „același loc”. Aici a...a[n ] – o anumită matrice și a[ m]... a[ n] (m = [ nDIV 2] + 1) formează deja o piramidă, deoarece indicii i si j , satisfacand relatia j = 2 i (sau j = 2 i + 1), pur și simplu nu există. 44 12 18
44 55 12 42 94 18 67
FIGURA 2.2 SELECTAREA CEI MICI CHEIE. 12 18
44 12 18 67
44 55 12 42 94 18 67
FIGURA 2.3. UMPLEREA GĂURILOR. Aceste elemente formează, parcă, stratul inferior al arborelui binar corespunzător (vezi Figura 2.4.), nu este necesară nicio ordonare pentru ele. Piramida se extinde acum spre stânga; de fiecare dată când un nou element este adăugat și mutat în poziția sa corectă. Piramida rezultată este prezentată în Figura 2.4. FIGURA 2.4 MATRICE REPREZENTATĂ CA UN ARBOR BINAR. PROGRAMUL 2.7. HEARSORT. I,X,L,N,R:INTEGER; A:RAY OF INTEGER; PROCEDURA SIFT(L,R: INTEGER); WRITELN("Introduceți lungimea matricei"); WRITELN("Introduceți matricea"); PENTRU I:=1 TO N DO WRITELN(‘Rezultat:”); PENTRU I:=1 TO N DO SFÂRŞIT. Analiza heapsort. Heapsort foarte eficient pentru un număr mare de elemente n; mai mare n , cu atât funcționează mai bine. În cel mai rău caz ai nevoie n /2 trepte de schimbare, acestea schimbă elementele prin log(n/2), log(n/2 – 1), … , log(n – 1) poziții (logaritmul la [baza 2] este „taiat” la următorul număr întreg mai mic). Prin urmare, faza de sortare va fi n – 1 schimburi cu cea mai mare log(n-1), log(n -2), … , 1 mișcări. Se poate concluziona că chiar și în cel mai rău caz posibil Heapsort va necesita n* logn trepte. Performanța excelentă în astfel de cazuri este una dintre proprietățile atractive Heapsort. 2.2.3. Sortați după împărțire
.
Această metodă de sortare îmbunătățită se bazează pe schimb. Aceasta este cea mai bună metodă de sortare a matricelor cunoscută în prezent. Performanța sa este atât de impresionantă încât inventatorul C. Hoare a numit această metodă quicksort ( Sortare rapida) În Quicksort se bazează pe considerația că pentru a obține cea mai bună eficiență este mai bine să facem mai întâi permutări pe distanțe mari. Să presupunem că avem n elemente dispuse prin chei în ordine inversă. Ele pot fi sortate după n /2 schimburi, mai întâi schimbați cel din stânga cu cel din dreapta și apoi mutați succesiv din ambele părți. Acest lucru este posibil atunci când știm că ordinea este cu adevărat inversată. Cu toate acestea, algoritmul rezultat poate să nu aibă succes, ceea ce, de exemplu, se întâmplă în cazul respectiv n chei identice: pentru a separa ai nevoie n /2 schimburi. Aceste schimburi inutile pot fi evitate dacă operatorii de căutare sunt înlocuiți cu: În acest caz x nu funcționează ca o barieră pentru două vederi. Ca rezultat, scanările matricei cu toate cheile identice vor avea ca rezultat un salt peste granițele matricei. Scopul nostru nu este doar să împărțim matricea originală de elemente în părți, ci și să o sortăm. Vom aplica procesul de separare celor două părți rezultate până când fiecare parte este formată dintr-un singur element. Aceste acțiuni sunt descrise în programul 2.8. PROGRAMUL 2.8. SORTARE RAPIDA. A:RAY OF INTEGER; PROCEDURA SORT(L,R: INTEGER); I,J,X,W: INTEGER; X:=A[(L+R) DIV 2]; WRITELN("Introduceți lungimea matricei"); WRITELN("Introduceți matricea"); FOR I:=1 TO N DO READ(A[I]); WRITELN("Rezultat:"); PENTRU I:=1 TO N DO SFÂRŞIT. Analiză de sortare rapidă . Procesul de separare decurge astfel: prin alegerea unei anumite valori la limită X , apoi parcurgem întregul tablou. În acest caz, se realizează exact n comparatii. Numărul așteptat de schimburi este media acestor valori așteptate pentru toate limitele posibile X. N*(n-1)/2n-(2n2-3n+1)/6n = (n-1/n)/6 (2,20.) Dacă am putea alege întotdeauna mediana ca limită, atunci fiecare proces de divizare ar împărți matricea în două jumătăți, iar sortarea ar necesita doar n* autentificare abordari. Ca urmare, numărul total de comparații ar fi egal cu n* autentificare , iar numărul total de schimburi este n*log(n ) /6. Dar probabilitatea acestui lucru este doar 1/ n. Principalul dezavantaj Sortare rapida – productivitate insuficient de mare cu mici n , totuși, aceasta este problema cu toate metodele avansate, unul dintre avantaje este că pentru prelucrarea pieselor mici, una dintre metodele de sortare directă poate fi inclusă cu ușurință în ea. Teste
.
Ideea includerii directe a sortării unei matrice este aceea
într-o succesiune sortată masi de lungime n (i = 0..n - 1), elementele sunt selectate secvenţial începând cu a doua (i
într-o succesiune sortată masi de lungime n (i=0..n-1), elementele sunt selectate secvenţial pornind de la primul (i într-o succesiune sortată masi de lungime n (i=0..n-1), elementele sunt selectate secvenţial începând cu a doua (i în succesiunea sortată masi de lungime n-1 (i=0..n-1), elementele sunt selectate secvenţial începând cu a doua (i Când sortați o matrice prin includere directă, căutarea locului pentru a include următorul element x din partea stângă a secvenței mas se poate termina în două situații:
a fost găsit un element al secvenței mas pentru care masi>x; s-a ajuns la capătul stâng al secvenței sortate din stânga.
s-a găsit un element al secvenţei mas pentru care masi s-a găsit un element al secvenţei mas pentru care masi Când sortați o matrice prin includere directă, se utilizează o tehnică de „barieră” pentru a urmări condiția de încheiere a scanării în stânga secvenței sortate. Esența sa este aceea
un element fictic X este adăugat la secvența originală din dreapta La începutul fiecărei etape de scanare în stânga părții sortate a matricei, elementul X este setat la valoarea elementului pentru care locația de inserare va fi. fi căutat. un element fictic X este adăugat la stânga secvenței originale La sfârșitul fiecărei etape de scanare în stânga părții sortate a matricei, elementul X este setat la valoarea elementului pentru care va fi locația de inserare. fi căutat. un element fictic X este adăugat la stânga secvenței inițiale La începutul fiecărei etape de scanare în stânga părții sortate a matricei, elementul X este setat la valoarea elementului pentru care va fi locația de inserare. să nu fie căutat. un element fictic X este adăugat la stânga secvenței inițiale La începutul fiecărei etape de scanare în stânga părții sortate a matricei, elementul X este setat la valoarea elementului pentru care va fi locația de inserare. fi căutat.
Sortarea unei matrice prin includere directă necesită în medie
N^2/2 mișcări. N^2/4 mişcări.
N^2 mișcări. N/4 mișcări. Alegeți opțiunea corectă de inserat în loc de semn de întrebare în fragmentul de cod pentru sortarea unei matrice prin includere directă:
Pentru i:=2 to Count do ÎNCEPE Tmp:=Arr[i]; j:=i-1; ÎNCEPE Arr:=Arr[j]; j:=j-1; Sfârşit; Arr:=Tmp; Sfârşit; În timp ce (j0) și (Arr[j] ) fac În timp ce (j>0) și (Arr[j]>Tmp) fac In timp ce
(j>0
)
și
(Arr[
j]
)
do
În timp ce (j=0) și (Arr[j]=Tmp) fac Algoritm pentru sortarea unui tablou după incluziuni binare
inserțiii
-
th
element într-o secvență gata făcută care nu este încă sortată, pentru a găsi un loc pentrui
-
th
inserții
i
-
th
i
-
th
element, este utilizată metoda de căutare binară pentru element.
inserțiii
-
th
element în secvența finală, care este deja sortată, pentru a găsi un loc pentrui
-
th
inserțiii
-
th
element într-o secvență gata făcută care nu este încă sortată, pentru a găsi un loc pentrui
-
th
element, se utilizează metoda Shell de căutare a unui element. Când sortați o matrice după incluziuni binare
total va fi produs
N
Buturuga
2
N
comparatii.
Buturuga
2
N
comparatii. Buturuga
2
(N/
2
)
comparatii. N
/2*log
2
N
comparatii. Se va schimba numărul de transferuri în sortarea matricei după incluziuni binare în raport cu numărul de comparații?
Vor fi mai multe va deveni mai mic Nu se va schimba.
Când sortați o matrice folosind metoda de includere binară, bucla interioară de căutare cu deplasare simultană ar trebui împărțită:
Căutarea binară găsește poziția de inserare, apoi toate elementele secvenței terminate situate în stânga acestei poziții sunt deplasate la dreapta. Căutarea binară găsește poziția de inserare, apoi toate elementele secvenței terminate situate în dreapta acestei poziții sunt deplasate la stânga. Căutarea binară găsește poziția de inserare, apoi toate elementele secvenței terminate situate în dreapta acestei poziții sunt deplasate la dreapta.
Căutarea binară găsește poziția de inserare, apoi toate elementele secvenței terminate situate în stânga acestei poziții sunt deplasate la stânga. Care este ideea de a sorta o matrice folosind metoda Shell?
Nu toate elementele secvenței sunt sortate, ci doar cele distanțate unele de altele la o anumită distanță mai mare decât h. Nu toate elementele secvenței sunt sortate, ci doar cele distanțate unele de altele la o anumită distanță mai mică decât h. Nu toate elementele secvenței sunt sortate, ci doar cele separate unele de altele la o anumită distanță h.
Nu toate elementele secvenței sunt sortate, ci doar h elemente. Când sortați o matrice folosind metoda Shell, la fiecare pas valoarea lui h se modifică până când devine (neapărat) egală cu
Dacă h=1, atunci algoritmul de sortare a matricei Shell degenerează în
sortare grămadă. sortarea după incluziuni directe.
sortare îmbinare. sortarea incluziunii binare. Când sortați o matrice folosind metoda Shell, distanțele dintre elementele comparate se pot schimba în moduri diferite. Singura cerință este aceea
ultimul pas trebuie să fie egal cu unu.
ultimul pas trebuie să fie zero. primul element este egal cu ultimul element. primul element este egal cu penultimul element. Eficiența sortării unui tablou folosind metoda Shell este explicată prin faptul că
Fiecare trecere folosește un număr foarte mare de elemente, iar ordonarea crește cu fiecare nouă privire asupra datelor. la fiecare trecere, elementele matricei nu sunt ordonate, iar ordonarea crește cu fiecare nouă privire asupra datelor.
fiecare trecere folosește un număr relativ mic de elemente, sau elementele matricei sunt deja în ordine relativă, iar ordonarea crește cu fiecare nouă privire asupra datelor. Ideea din spatele algoritmului de sortare cu selecție directă este aceea
La fiecare pas, partea dreaptă nesortată a matricei este scanată. Acesta caută următorul element maxim. Dacă este găsit, atunci este mutat în locul elementului din stânga din partea dreaptă nesortată a matricei. La fiecare pas, partea dreaptă nesortată a matricei este scanată. Acesta caută următorul element minim. Dacă nu este găsit, atunci este mutat în locul elementului din stânga din partea dreaptă nesortată a matricei. La fiecare pas, partea dreaptă nesortată a matricei este scanată. Acesta caută următorul element minim. Dacă este găsit, atunci este mutat în locul elementului din dreapta al părții din stânga nesortate a matricei. La fiecare pas, partea dreaptă nesortată a matricei este scanată. Acesta caută următorul element minim. Dacă este găsit, atunci este mutat în locul elementului din stânga din partea dreaptă nesortată a matricei.
Dacă sortarea de selecție este aplicată matricei „bdac”, se vor obține următoarele treceri
prima trecere: c d b A ; a doua trecere: a b b c; a treia trecere: a b c d.
dc; a treia trecere: a b c d.
prima trecere: a d b c; a doua trecere: a CDB ; a treia trecere: a b c d. prima trecere: a d b c; a doua trecere: a b d c; a treia trecere: d b c A .
La fel ca în sortarea unui tablou folosind metoda bubble, în sortarea unui tablou prin selecție directă, bucla exterioară
este executată de n ori, iar bucla interioară este executată de n/2 ori. rulează de n-1 ori și bucla interioară rulează de n ori. rulează de n-1 ori și bucla interioară rulează de n/2 ori.
este executată de n ori și bucla interioară este executată de n ori. Introduceți inegalitatea corectă în fragmentul de cod de sortare al matricei prin selecție directă, în loc de semnul întrebării:
pentru i:= 1 la n - 1 do ÎNCEPE min:= i; pentru j:= i + 1 la n do dacă?
apoi min:= j; t:= a[i]; a[i] := a; a := t Sfârşit; a > a[j]. A [
min ]
A [
j ].
Când sortați o matrice folosind metoda de selecție directă, în cel mai bun caz (când matricea originală este deja sortată), va trebui schimbată doar ?, iar fiecare operație de schimb necesită trei operații de transfer.
Introduceți opțiunea corectă în loc de semnul întrebării.
n-elemente. (n-1)-elemente.
n/2-elemente. 2*n-elemente. Algoritmul de sortare a matricei care utilizează metoda de selecție a piramidei este conceput pentru a sorta o secvență de numere care
sunt o reprezentare de memorie a unui arbore cu o structură specială - o piramidă.
sunt o reprezentare de memorie a unui arbore cu o structură specială - un arbore. sunt o reprezentare de memorie a unei piramide a unei structuri speciale - o piramidă. sunt o reflectare în memoria unui tufiș cu o structură specială - un copac. Imaginea prezintă mai mulți copaci, dintre care doar unul
este o piramidă.
T4.
Piramida prezentată în figură (una din patru) va fi reprezentată în memorie prin următorul tablou:
3, 2, 7, 11, 5, 8, 14, 9, 27.
2, 3, 5, 7, 8, 9, 11, 14, 27. 27, 14, 11, 9, 8, 7, 5, 3, 2. 27, 9, 14, 8, 5, 11, 7, 2, 3.
În fiecare dintre cei n pași necesari pentru a sorta o matrice folosind metoda de selecție a piramidei, aveți nevoie
n *log n comparații (binare). (jurnal n)/2comparații (binare). log n comparații (binare).
2 *log n comparații (binare). Ideea din spatele algoritmului de sortare a matricei de schimb direct este că
dacă numărul de poziție al elementului mai mare este mai mare decât numărul de poziție al elementului mai mic, atunci le schimbăm. dacă numărul de poziție al elementului mai mic este mai mare decât numărul de poziție al elementului mai mare, atunci nu le schimbăm. dacă numărul de poziție al elementului mai mic este mai mare decât numărul de poziție al elementului mai mare, atunci le lăsăm pe loc. dacă numărul de poziție al elementului mai mic este mai mare decât numărul de poziție al elementului mai mare, atunci le schimbăm.
Când utilizați metoda de sortare cu bule de matrice, necesită cel mult
n treceri. (n-1) trece.
n/2 treceri. 2*n pasaje. Când sortați o matrice folosind metoda schimbului direct sau metoda de sortare cu bule, după fiecare trecere prin tabel, se poate verifica dacă s-au făcut permutări în timpul acelei treceri. Dacă nu existau permutări, atunci asta înseamnă că
masa nu este sortată și necesită treceri suplimentare. masa este deja sortată și necesită treceri suplimentare. tabelul este deja sortat și nu sunt necesare alte treceri.
masa nu este sortată și nu sunt necesare alte treceri. Sortarea cu bule a unei matrice are o particularitate: un element este plasat din loc la sfârșitul matricei
ajunge la locul său într-o singură trecere.
ajunge la locul său în două treceri. ajunge la locul său în trei treceri. ajunge la locul său în N pasaje. Sortarea cu bule a unei matrice are o caracteristică: elementul este situat la începutul matricei
ajunge foarte repede la locul ei. ajunge foarte încet la locul ei.
nu ajunge la locul ei. ajunge la mijlocul matricei. Metoda de sortare a matricei interne se bazează pe procedura de îmbinare
două mese ordonate.
o masă ordonată. trei mese ordonate. două mese neordonate. Esența sortării prin îmbinare este că tabelul sortat este împărțit în grupuri egale de elemente. Grupurile sunt ordonate și apoi
fuzionează în perechi, formând trei grupuri noi care conțin de trei ori mai multe elemente. îmbina în perechi pentru a forma două grupuri noi care conțin de două ori mai multe elemente. fuzionează în perechi, formând noi grupuri care conțin de trei ori mai multe elemente. îmbina în perechi pentru a forma noi grupuri care conțin de două ori mai multe elemente.
În testele propuse, răspunsurile corecte sunt scrise cu caractere cursive. Concluzie
.
Acest curs examinează problemele de sortare și formularea problemei sortării tablourilor. Și, de asemenea, partea principală este dedicată luării în considerare a metodelor: și anume, metode simple de sortare (sortare prin includere directă, sortare prin selecție directă, sortare prin schimb direct) și metode îmbunătățite de sortare a tablourilor (metoda Shell, sortare folosind arbore, sortare folosind separare). Se propune o analiză pentru fiecare dintre metodele de sortare a matricei. A dezvoltat sarcini de testare pentru sortarea matricelor (30 de sarcini).http://ru.wikipedia.org Articolul discută unii dintre cei mai populari algoritmi de sortare pentru matrice, folosiți atât practic, cât și în scopuri educaționale. Aș dori să fac imediat o rezervă că toți algoritmii luați în considerare sunt mai lenți decât metoda clasică de sortare a unui tablou printr-o listă de valori, dar cu toate acestea, merită atenție. Există mult text, așa că pentru fiecare algoritm îi descriu pe cei mai de bază. 1. Algoritmul „Sortare după alegere”. Este unul dintre cei mai simpli algoritmi de sortare a matricei. Ideea este să parcurgeți matricea și să căutați de fiecare dată elementul minim al matricei, schimbându-l cu elementul de pornire al părții nesortate a matricei. Pe matrice mici poate fi chiar mai eficient decât algoritmii de sortare mai complecși, dar în orice caz pierde pe matrice mari. Numărul de schimburi de elemente în comparație cu algoritmul „bulă” este N/2, unde N este numărul de elemente ale matricei. Algoritm: //Sortează după selecție (--- Funcție Sortează după selecție (Matrice de valori) Min = 0; Pentru i = 0 După Matrice.VBoundary() Bucla Min = i; Pentru j = i + 1 Prin Buclă Array.VBoundary() / / Căutați elementul minim în matrice If Array[j]< Массив[Мин] Тогда
Мин = j;
КонецЕсли;
КонецЦикла;
Если Массив [Мин] = Массив [i] Тогда //Если мин. элемент массива = первому элементу неотс. части массива, то пропускаем.
Продолжить;
КонецЕсли;
Смена = Массив[i]; //Производим замену элементов массива.
Массив[i] = Массив[Мин];
Массив[Мин] = Смена;
КонецЦикла;
Возврат Массив;
КонецФункции
2. Algoritmul „Bubble sort”. Poate cel mai faimos algoritm, folosit în scopuri educaționale, este prea lent pentru utilizare practică. Algoritmul stă la baza unor algoritmi mai complexi: „Shaker sort”, „Pyramid sort”, „Quick sort”. Este de remarcat faptul că unul dintre cei mai rapizi algoritmi, „Algoritmul rapid”, a fost dezvoltat prin modernizarea unuia dintre cei mai proasți algoritmi, sortarea „Bubble Sort” și „Shaker”. Semnificația algoritmului este că cele mai „ușoare” elemente ale matricei „plutesc”, iar cele „mai grele” „se scufundă”. De aici și numele „Bubble Sort” Algoritm: //Bubble Sort (--- Funcție Bubble Sort(Matrice de valori) Pentru i = 0 Prin Array.InBorder() Bucla Pentru j = 0 Prin Array.InBorder() - i - 1 Buclă If Array[j] > Array Then Replacement = Array [j]; Array = EndIf; 3. Algoritmul „Shaker sort” (Shuffle sort, Bidirectional bubble sort). Algoritmul este o versiune a sortării anterioare - „sortare cu bule”. Principala diferență este că în sortarea clasică cu bule există o mișcare unidirecțională a elementelor de jos în sus, în timp ce în sortarea cu agitare, mișcarea are loc mai întâi de jos în sus și apoi de sus în jos. Algoritmul este același cu sortarea cu bule + se adaugă un ciclu de sus în jos. În exemplul de mai jos, există o îmbunătățire a sortării agitatorului. Spre deosebire de cea clasică, se folosesc de 2 ori mai puține iterații. //Sortare după amestecare (Shaker-Sort) (--- Funcție Sortare după amestecare (Matrice de valori) Pentru i = 0 BY Array.VBoundary()/2 Loop nIter = 0; conIter = Array.VBoundary(); While nIter Array [nIter+ 1] Apoi Înlocuire = Array[nIter] = Array[nIter + 1] = Înlocuire nIter = nIter + 1;//Mutați poziția cu un pas înainte //Treceți cu end If Array[conIter]; > Array[conIter] Then Replacement = Array[conIter - 1] = Replacere (Înlocuire) EndCycle; 4. Algoritmul „Sortare pitici”. Algoritmul este numit atât de ciudat datorită omului de știință olandez Dick Grun. Sortarea gnomilor se bazează pe tehnica folosită de gnomul de grădină olandez comun (tuinkabouter olandez). Aceasta este metoda prin care un gnom de grădină sortează o linie de ghivece de flori. În esență, el se uită la ghivecele de grădină următoare și anterioare: dacă sunt în ordinea corectă, face un pas înainte, în caz contrar, le schimbă și face un pas înapoi. Condiții limită: dacă nu există o oală anterioară, face un pas înainte; dacă nu există următoarea oală, s-a terminat. Aceasta este de fapt întreaga descriere a algoritmului „Sortarea piticilor”. Interesant este că algoritmul nu conține bucle imbricate, ci sortează întregul tablou într-o singură trecere. // Sortare pitică (--- Funcția DwarvenSort(Matrice de valori) i = 1; j = 2; În timp ce i< Массив.Количество() Цикл // Сравнение < - Сортировка по возрастанию, >- descendent If Array i = j; j = j + 1; Altfel Înlocuire = Matrice[i]; Matrice[i] = Matrice; Array = Înlocuire; i = i - 1; Dacă i = 0, atunci i = j; j = j + 1; endIf; endIf; EndCycle; Return Array; EndFunction //---) 5. Algoritmul „Sortare prin inserare”. Acesta este un algoritm de sortare simplu. Ideea este că la fiecare pas luăm un element, căutăm o poziție pentru el și îl introducem în locul potrivit. 6. Algoritmul „Merge sort”. Un algoritm interesant în ceea ce privește implementarea și ideea. Semnificația sa este de a împărți matricea în subdiviziuni până când lungimea fiecărei subdiviziuni este egală cu 1. Apoi susținem că o astfel de subdivizie este sortată. Apoi îmbinăm subtabelele rezultate, comparând și sortând simultan valorile elementului subgrupului cu element. p/s Nu am putut introduce aici un desen cu o diagramă mai vizuală, este pătat în mod constant. Dar este clar vizibil în blocul de capturi de ecran de mai jos. Puteți vedea cum funcționează algoritmul. //Imbinare sortare (--- Funcția MergeSort(Value Array) If Array.Count() = 1 Then Return Array; endIf; PointBreak = Array.Count() / 2; lArray = matrice nouă; prArray = matrice nouă; Pentru Count = 0 BY Array.VBoundary() Cycle If Count< ТочкаРазрыв Тогда
лМассив.Добавить(Массив[Сч]);
Иначе
прМассив.Добавить(Массив[Сч]);
КонецЕсли;
КонецЦикла;
Возврат Слияние(СортировкаСлиянием(лМассив),СортировкаСлиянием(прМассив));
КонецФункции
Функция Слияние(массив1,массив2)
a = 0;
b = 0;
слМассив = Новый Массив;
Для Сч = 0 ПО (Массив1.Количество() + Массив2.Количество())-1 Цикл
слМассив.Добавить();
КонецЦикла;
Для i = 0 ПО (массив1.Количество() + массив2.Количество())-1 Цикл
Если b < массив2.Количество() И a < массив1.Количество() Тогда
Если (массив1[a] >matrice2[b]) ȘI (b< массив2.Количество()) Тогда
слМассив[i] = массив2[b];
b = b + 1;
Иначе
слМассив[i] = массив1[a];
a = a + 1;
КонецЕсли;
Иначе
Если b < массив2.количество() Тогда
слМассив[i] = массив2[b];
b = b + 1;
Иначе
слМассив[i] = массив1[a];
a = a + 1;
КонецЕсли;
КонецЕсли;
КонецЦикла;
Возврат слМассив;
КонецФункции
//---}
7. Algoritmul „Shell Sorting”. Algoritmul este numit după omul de știință american Donald Schell. În esență, acest algoritm este un algoritm îmbunătățit de sortare prin inserție. Scopul algoritmului este de a compara nu numai elementele situate unul lângă celălalt, ci și la o anumită distanță. În primul rând, este selectat un Step - un anumit interval prin care elementele matricei vor fi comparate la fiecare iterație. De obicei este definit astfel: Exemplu: 10
,2
,3
,1,14
,5
,7
,12 2. Pasul = 2 3
,1
,7
,2
,10
,5
,14
,12
3. Pasul = 1 1,2,3,5,7,10,12,14 8. Algoritmul „Sortare rapidă”. Cel mai popular și folosit algoritm în practică. Este unul dintre cei mai eficienți algoritmi de sortare a datelor. //Algoritmul „Sortare rapidă” ( Procedura b_Sort(Array, LowerLimit, UpperLimit) i = LowerLimit; j = UpperLimit; m = Array[Integr((i+j)/2)]; While True Loop While Array[i]< m Цикл
i = i + 1;
КонецЦикла;
Пока Массив[j] >m Ciclul j = j - 1; EndCycle; Dacă i > j Atunci Avort; endIf; EndCycle; Dacă LowerLimit< j Тогда
б_Сортировка(Массив,НижнийПредел,j);
КонецЕсли;
Если i < ВерхнийПредел Тогда
б_Сортировка(Массив,i,ВерхнийПредел);
КонецЕсли;
КонецПроцедуры
Функция БыстраяСортировка(Массив)
НижняяГраница = 0;
ВерхняяГраница = Массив.ВГраница();
б_Сортировка(Массив,НижняяГраница,ВерхняяГраница);
Возврат Массив;
КонецФункции
//---}
9. Sortare clasică de matrice în 1s. Trecem tabloul la o listă de valori. Sortăm folosind metoda standard „Sort”. //Sortați după o listă de valori (--- Funcția Sortare după o listă de valori (Matrice de valori) mListValues = New ListValues; mListValues.LoadValues(Array); mListValues.SortByValue(SortDirection.Asc); Returnează mListValues.UnloadValues(); Toată sortarea poate fi accelerată prin plasarea codului în bucle de 1 linie. Dar pentru lizibilitate, am lăsat-o așa.
Am scris o procesare care implementează toți algoritmii de mai sus și, de asemenea, acceptă animația dinamică a procesului de sortare (Cu excepția sortării standard 1c) .
- Când începe procesarea, se formează automat o matrice de numere aleatoare de la 0 la 100 cu o dimensiune de 100 de elemente. Redarea dinamică a procesului de sortare reduce foarte mult performanța, dar puteți vedea clar cum funcționează algoritmul.1. Sortarea sarcinilor.
1.1.Dispoziții generale.
1.2. Enunțarea problemei sortării tablourilor.
2. Metode de sortare a tablourilor.
2.1. Metode simple de sortare a tablourilor.
2.1.1. Sortarea folosind includerea directă.
2.1.2.Sortarea folosind selecția directă.
2.2. Metode îmbunătățite pentru sortarea matricelor.
2.2.1.Metoda Shell.
1. Găsiți elementul minim din matrice.
2. Schimbați elementele minime și primele.
3. Căutăm din nou elementul minim în partea nesortată a matricei
4. Schimbați al doilea element al matricei și cel minim găsit, deoarece primul element al matricei este partea sortată.
5. Căutăm valorile minime și schimbăm elementele până când matricea este sortată până la sfârșit.
1. Fiecare element al matricei este comparat cu următorul și dacă element[i] > element este înlocuit. Astfel, cele mai „ușoare” elemente „plutesc” - se deplasează la începutul listei, iar cea mai grea „chiuvetă” - se deplasează la sfârșit.
2. Repetați Pasul 1 de n-1 ori, unde n este Array.Quantity ().
Dick Grun
Un exemplu elementar: Când joci prost, trageți o carte din pachet și o introduceți în locul potrivit în ordine crescătoare din cărțile pe care le aveți. Sau
în magazin ți-au dat schimb pentru 550 de ruble - o bancnotă este 500, cealaltă este 50. Te uiți în portofel și sunt bancnote în valori de 10.100.1000. Introdu o factură
în valoare de 50 de ruble. între bancnote de 10r și 100r și o bancnotă de 500 de ruble între bancnote de 100r și 1000r. Se dovedește 10,50,100,500,1000 - Poftim
și algoritmul Insertion Sort.
Astfel, cu fiecare pas al algoritmului, trebuie să sortați subbarra de date și să introduceți valoarea în locul potrivit.
//Inserție Sortare (--- Funcție Inserție Sort(Matrice de valori) Pentru i = 0 Prin Matrice.BBorder()-1 Cheie buclă = i + 1; Înlocuiește = Matrice[Cheie]; j = i + 1; While j > 0 Și Înlocuire< Массив Цикл
Массив[j] = Массив;
Замена = j - 1;
Ключ = j - 1;
j = j - 1;
КонецЦикла;
Массив[Ключ] = Замена;
КонецЦикла;
Возврат Массив;
КонецФункции
//---}
Pentru prima iterație, Step = Object(Array.Quantity()/2), pentru iterațiile ulterioare, Step = Object(Step/2). Acestea. treptat pasul se reduce și când pasul este egal cu 1 va avea loc ultima comparație și matricea va fi sortată.
Dată o matrice (10,5,3,1,14,2,7,12).
1. Pasul = 4.
Sortăm după inserții simple la fiecare 4 grupuri de 2 elemente (10,14)(5,2)(3,7)(1,12)
Sortăm după inserții simple la fiecare 2 grupuri de 4 elemente (10,3,14,7)(2,1,5,12)
Sortăm după inserții simple fiecare 1 grup de 8 elemente.
//Shell Sort (--- Funcție Shell Sort(Value Array) Step = Integer(Array.Quantity()/2); While Step > 0 Cycle i = 0; While i< (Массив.Количество() - Шаг) Цикл
j = i;
Пока j >= 0 AND Array[j] > Array Loop Replacement = Array[j]; Matrice[j] = Matrice; Array = Înlocuire; j = j - 1; Dacă ApplyDisplaySortThenDisplaySortChart(Array); endIf; EndCycle; i = i + 1; EndCycle; Pas = Obiect (Pasul/2); UserInterruptHandling(); EndCycle; Return Array; EndFunction //---)
Întreaga esență a algoritmului se rezumă la împărțirea unei probleme complexe în unele mici și rezolvarea lor separat. Este selectat un anumit punct de referință și toate valorile care sunt mai mici sunt aruncate la stânga, toate celelalte la dreapta. Apoi, pentru fiecare parte primită, faceți același lucru, până când nu mai este posibilă împărțirea părților. La sfârșit, obținem o mulțime de părți sortate care trebuie doar lipite într-un singur întreg.
-Pentru a crea o altă matrice, trebuie să faceți clic pe butonul „Creați matrice RNG”, puteți selecta și intervalul necesar.
-Pentru a activa animația dinamică, trebuie să bifați caseta „Afișează sortarea în diagramă”. Vă sfătuiesc să bifați caseta pentru algoritmi ineficienți atunci când dimensiunea matricei este de până la 100 de elemente, altfel veți fi prea bătrân pentru a aștepta sortarea :)