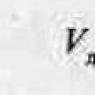Determine the rank of the matrix using the method of elementary transformations. The concept of matrix rank

>>Matrix rank

Matrix rank

Determining the rank of a matrix

Consider a rectangular matrix. If in this matrix we select arbitrarily k lines and k columns, then the elements at the intersection of the selected rows and columns form a square matrix of kth order. The determinant of this matrix is ​​called minor of kth order matrix A. Obviously, matrix A has minors of any order from 1 to the smallest of the numbers m and n. Among all nonzero minors of the matrix A, there is at least one minor whose order is the greatest. The largest of the non-zero minor orders of a given matrix is ​​called rank matrices. If the rank of matrix A is r, this means that matrix A has a non-zero minor of order r, but every minor of order greater than r, is equal to zero. The rank of matrix A is denoted by r(A). Obviously, the relation holds

Calculating the rank of a matrix using minors

The rank of the matrix is ​​found either by the method of bordering minors or by the method of elementary transformations. When calculating the rank of a matrix using the first method, you should move from lower order minors to higher order minors. If a minor D of the kth order of the matrix A, different from zero, has already been found, then only the (k+1) order minors bordering the minor D require calculation, i.e. containing it as a minor. If they are all equal to zero, then the rank of the matrix is k.

Example 1.Find the rank of the matrix using the method of bordering minors

.

Solution.We start with 1st order minors, i.e. from the elements of matrix A. Let us choose, for example, a minor (element) M 1 = 1, located in the first row and first column. Bordering with the help of the second row and third column, we obtain a minor M 2 = different from zero. We now turn to the 3rd order minors bordering M2. There are only two of them (you can add a second or fourth column). Let's calculate them: = 0. Thus, all bordering minors of the third order turned out to be equal to zero. The rank of matrix A is two.

Calculating the rank of a matrix using elementary transformations

ElementaryThe following matrix transformations are called:

1) permutation of any two rows (or columns),

2) multiplying a row (or column) by a non-zero number,

3) adding to one row (or column) another row (or column), multiplied by a certain number.

The two matrices are called equivalent, if one of them is obtained from the other using a finite set of elementary transformations.

Equivalent matrices are not, generally speaking, equal, but their ranks are equal. If matrices A and B are equivalent, then it is written as follows: A~B.

CanonicalA matrix is ​​a matrix in which at the beginning of the main diagonal there are several ones in a row (the number of which can be zero), and all other elements are equal to zero, for example,

.

Using elementary transformations of rows and columns, any matrix can be reduced to canonical. The rank of a canonical matrix is ​​equal to the number of ones on its main diagonal.

Example 2Find the rank of a matrix

A=

and bring it to canonical form.

Solution. From the second line, subtract the first and rearrange these lines:

.

Now from the second and third lines we subtract the first, multiplied by 2 and 5, respectively:

;

subtract the first from the third line; we get a matrix

B = ,

which is equivalent to matrix A, since it is obtained from it using a finite set of elementary transformations. Obviously, the rank of matrix B is 2, and therefore r(A)=2. Matrix B can easily be reduced to canonical. By subtracting the first column, multiplied by suitable numbers, from all subsequent ones, we turn to zero all the elements of the first row, except the first, and the elements of the remaining rows do not change. Then, subtracting the second column, multiplied by suitable numbers, from all subsequent ones, we turn to zero all elements of the second row, except the second, and obtain the canonical matrix:

.

Let some matrix be given:

.

Let us select in this matrix arbitrary strings and arbitrary columns
. Then the determinant th order, composed of matrix elements
, located at the intersection of selected rows and columns, is called a minor th order matrix
.

Definition 1.13. Matrix rank
is the largest order of the non-zero minor of this matrix.

To calculate the rank of a matrix, one should consider all its minors of the lowest order and, if at least one of them is different from zero, proceed to considering the minors of the highest order. This approach to determining the rank of a matrix is ​​called the bordering method (or the method of bordering minors).

Problem 1.4. Using the method of bordering minors, determine the rank of the matrix
.

.

Consider first-order edging, for example,
. Then we move on to consider some second-order edging.

For example,
.

Finally, let's analyze the third-order bordering.

.

So the highest order of a non-zero minor is 2, hence
.

When solving Problem 1.4, you can notice that a number of second-order bordering minors are nonzero. In this regard, the following concept applies.

Definition 1.14. A basis minor of a matrix is ​​any non-zero minor whose order is equal to the rank of the matrix.

Theorem 1.2.(Basis minor theorem). The basis rows (basis columns) are linearly independent.

Note that the rows (columns) of a matrix are linearly dependent if and only if at least one of them can be represented as a linear combination of the others.

Theorem 1.3. The number of linearly independent matrix rows is equal to the number of linearly independent matrix columns and is equal to the rank of the matrix.

Theorem 1.4.(Necessary and sufficient condition for the determinant to be equal to zero). In order for the determinant -th order was equal to zero, it is necessary and sufficient that its rows (columns) be linearly dependent.

Calculating the rank of a matrix based on its definition is too cumbersome. This becomes especially important for matrices of high orders. In this regard, in practice, the rank of a matrix is ​​calculated based on the application of Theorems 10.2 - 10.4, as well as the use of the concepts of matrix equivalence and elementary transformations.

Definition 1.15. Two matrices
And are called equivalent if their ranks are equal, i.e.
.

If matrices
And are equivalent, then note
 .

Theorem 1.5. The rank of the matrix does not change due to elementary transformations.

We will call elementary matrix transformations
any of the following operations on a matrix:

Replacing rows with columns and columns with corresponding rows;

Rearranging matrix rows;

Crossing out a line whose elements are all zero;

Multiplying a string by a number other than zero;

Adding to the elements of one line the corresponding elements of another line multiplied by the same number
.

Corollary of Theorem 1.5. If matrix
obtained from matrix using a finite number of elementary transformations, then the matrix
And are equivalent.

When calculating the rank of a matrix, it should be reduced to a trapezoidal form using a finite number of elementary transformations.

Definition 1.16. We will call trapezoidal a form of matrix representation when in the bordering minor of the highest order non-zero, all elements below the diagonal ones vanish. For example:

.

Here
, matrix elements
go to zero. Then the form of representation of such a matrix will be trapezoidal.

As a rule, matrices are reduced to a trapezoidal shape using the Gaussian algorithm. The idea of ​​the Gauss algorithm is that, by multiplying the elements of the first row of the matrix by the corresponding factors, it is achieved that all elements of the first column located below the element
, would turn to zero. Then, multiplying the elements of the second column by the corresponding factors, we ensure that all elements of the second column located below the element
, would turn to zero. Then proceed in the same way.

Problem 1.5. Determine the rank of a matrix by reducing it to a trapezoidal shape.

.

To make it easier to use the Gaussian algorithm, you can swap the first and third lines.








.

It's obvious that here
. However, to bring the result to a more elegant form, you can further continue transforming the columns.










.

We will also consider an important practical application of the topic: study of a system of linear equations for consistency.

What is the rank of a matrix?

The humorous epigraph of the article contains a large amount of truth. We usually associate the word “rank” with some kind of hierarchy, most often with a career ladder. The more knowledge, experience, abilities, connections, etc. a person has. – the higher his position and range of opportunities. In youth terms, rank refers to the general degree of “steepness.”

And our mathematical brothers live by the same principles. Let's take a few random ones for a walk zero matrices:

Let's think about it, if in the matrix all zeros, then what rank can we talk about? Everyone is familiar with the informal expression “total zero”. In the society of matrices everything is exactly the same:

Rank of the zero matrixany size equals zero.

Note : The zero matrix is ​​denoted by the Greek letter "theta"

In order to better understand the rank of the matrix, hereinafter I will use materials to help analytical geometry. Consider zero vector our three-dimensional space, which does not set a specific direction and is useless for building affine basis. From an algebraic point of view, the coordinates of this vector are written in matrix“one by three” and logical (in the indicated geometric sense) assume that the rank of this matrix is ​​zero.

Now let's look at a few non-zero column vectors And row vectors:


Each instance has at least one non-zero element, and that's something!

The rank of any non-zero row vector (column vector) is equal to one

And generally speaking - if in the matrix arbitrary sizes there is at least one non-zero element, then its rank not less units.

Algebraic row vectors and column vectors are to a certain extent abstract, so let's turn again to the geometric association. Non-zero vector sets a very definite direction in space and is suitable for constructing basis, therefore the rank of the matrix will be considered equal to one.

Theoretical information : in linear algebra, a vector is an element of a vector space (defined through 8 axioms), which, in particular, can represent an ordered row (or column) of real numbers with the operations of addition and multiplication by a real number defined for them. More detailed information about vectors can be found in the article Linear transformations.

linearly dependent(expressed through each other). From a geometric point of view, the second line contains the coordinates of the collinear vector , which did not advance the matter at all in building three-dimensional basis, being in this sense superfluous. Thus, the rank of this matrix is ​​also equal to one.

Let's rewrite the coordinates of the vectors into columns ( transpose the matrix):

What has changed in terms of rank? Nothing. The columns are proportional, which means the rank is equal to one. By the way, note that all three lines are also proportional. They can be identified with the coordinates three collinear vectors of the plane, of which only one useful for constructing a "flat" basis. And this is entirely consistent with our geometric sense of rank.

An important statement follows from the above example:

The rank of the matrix in rows is equal to the rank of the matrix in columns. I already mentioned this a little in the lesson about effective methods for calculating the determinant.

Note : linear dependence of rows implies linear dependence of columns (and vice versa). But in order to save time, and out of habit, I will almost always talk about linear dependence of strings.

Let's continue training our beloved pet. Let's add the coordinates of another collinear vector to the matrix in the third row :

Did he help us in constructing a three-dimensional basis? Of course not. All three vectors walk back and forth along the same path, and the rank of the matrix is ​​equal to one. You can take as many collinear vectors as you like, say, 100, put their coordinates into a “one hundred by three” matrix, and the rank of such a skyscraper will still remain one.

Let's get acquainted with the matrix, the rows of which linearly independent. A pair of non-collinear vectors is suitable for constructing a three-dimensional basis. The rank of this matrix is ​​two.

What is the rank of the matrix? The lines don’t seem to be proportional... so, in theory, they are three. However, the rank of this matrix is ​​also two. I added the first two lines and wrote the result at the bottom, i.e. linearly expressed the third line through the first two. Geometrically, the rows of the matrix correspond to the coordinates of three coplanar vectors, and among this three there are a pair of non-collinear comrades.

As you can see, linear dependence in the considered matrix is ​​not obvious, and today we will learn how to bring it out into the open.

I think many people can guess what the rank of a matrix is!

Consider a matrix whose rows linearly independent. Vectors form affine basis, and the rank of this matrix is ​​three.

As you know, any fourth, fifth, tenth vector of three-dimensional space will be linearly expressed in terms of basis vectors. Therefore, if you add any number of rows to a matrix, then its rank will still be equal to three.

Similar reasoning can be carried out for matrices of larger sizes (of course, without any geometric meaning).

Definition : The rank of a matrix is ​​the maximum number of linearly independent rows. Or: The rank of a matrix is ​​the maximum number of linearly independent columns. Yes, their number is always the same.

An important practical guideline also follows from the above: the rank of the matrix does not exceed its minimum dimension. For example, in the matrix four rows and five columns. The minimum dimension is four, therefore, the rank of this matrix certainly will not exceed 4.

Designations: in world theory and practice there is no generally accepted standard for designating the rank of a matrix; most often you can find: - as they say, an Englishman writes one thing, a German another. Therefore, based on the famous joke about American and Russian hell, let’s denote the rank of the matrix with a native word. For example: . And if the matrix is ​​“unnamed”, of which there are many, then you can simply write .

How to find the rank of a matrix using minors?

If my grandmother had a fifth column in her matrix, then she would have to calculate another minor of the 4th order (“blue”, “raspberry” + 5th column).

Conclusion: the maximum order of a non-zero minor is three, which means .

Perhaps not everyone has fully comprehended this phrase: a minor of the 4th order is equal to zero, but among the minors of the 3rd order there was a non-zero one - therefore the maximum order non-zero minor and equals three.

The question arises, why not immediately calculate the determinant? Well, firstly, in most tasks the matrix is ​​not square, and secondly, even if you get a non-zero value, the task will most likely be rejected, since it usually involves a standard “bottom-up” solution. And in the example considered, the zero determinant of the 4th order allows us to state that the rank of the matrix is ​​only less than four.

I must admit, I came up with the problem I analyzed myself in order to better explain the method of bordering minors. In real practice, everything is simpler:

Example 2

Find the rank of a matrix using the edge minors method

The solution and answer are at the end of the lesson.

When does the algorithm work fastest? Let's return to the same four-by-four matrix. . Obviously, the solution will be the shortest in the case of “good” corner minors:

And, if , then , otherwise – .

The thinking is not at all hypothetical - there are many examples where the whole matter is limited only to angular minors.

However, in some cases another method is more effective and preferable:

How to find the rank of a matrix using the Gaussian method?

The paragraph is intended for readers who are already familiar with Gaussian method and more or less got their hands on it.

From a technical point of view, the method is not novel:

1) using elementary transformations, we reduce the matrix to a stepwise form;

2) the rank of the matrix is ​​equal to the number of rows.

It is absolutely clear that using the Gaussian method does not change the rank of the matrix, and the essence here is extremely simple: according to the algorithm, during elementary transformations, all unnecessary proportional (linearly dependent) rows are identified and removed, resulting in a “dry residue” - the maximum number of linearly independent rows.

Let's transform the old familiar matrix with the coordinates of three collinear vectors:

(1) The first line was added to the second line, multiplied by –2. The first line was added to the third line.

(2) Zero lines are removed.

Thus, there is one line left, hence . Needless to say, this is much faster than calculating nine zero minors of the 2nd order and only then drawing a conclusion.

I remind you that in itself algebraic matrix nothing can be changed, and transformations are performed only for the purpose of determining the rank! By the way, let’s dwell once again on the question, why not? Source matrix carries information that is fundamentally different from the information of the matrix and row. In some mathematical models (no exaggeration), the difference in one number can be a matter of life and death. ...I remembered primary and secondary school mathematics teachers who mercilessly cut grades by 1-2 points for the slightest inaccuracy or deviation from the algorithm. And it was terribly disappointing when, instead of a seemingly guaranteed “A”, it turned out “good” or even worse. Understanding came much later - how else to entrust satellites, nuclear warheads and power plants to a person? But don't worry, I don't work in these areas =)

Let's move on to more meaningful tasks, where, among other things, we will get acquainted with important computational techniques Gauss method:

Example 3

Find the rank of a matrix using elementary transformations

Solution: a “four by five” matrix is ​​given, which means that its rank is certainly no more than 4.

In the first column, there is no 1 or –1, therefore, additional actions are required to obtain at least one unit. Throughout the existence of the site, I have been repeatedly asked the question: “Is it possible to rearrange columns during elementary transformations?” Here, we rearranged the first and second columns, and everything is fine! In most tasks where it is used Gaussian method, the columns can indeed be rearranged. BUT NOT NEEDED. And the point is not even in possible confusion with variables, the point is that in the classical course of higher mathematics this action is traditionally not considered, so such a nod will be looked at VERY crookedly (or even forced to redo everything).

The second point concerns numbers. As you make your decision, it is helpful to use the following rule of thumb: elementary transformations should, if possible, reduce the matrix numbers. After all, it is much easier to work with one, two, three than, for example, with 23, 45 and 97. And the first action is aimed not only at obtaining a one in the first column, but also at eliminating the numbers 7 and 11.

First the complete solution, then comments:

(1) The first line was added to the second line, multiplied by –2. The first line was added to the third line, multiplied by –3. And to the heap: the 1st line was added to the 4th line, multiplied by -1.

(2) The last three lines are proportional. The 3rd and 4th lines were removed, the second line was moved to the first place.

(3) The first line was added to the second line, multiplied by –3.

The matrix reduced to echelon form has two rows.

Answer:

Now it's your turn to torture the four-by-four matrix:

Example 4

Find the rank of a matrix using the Gaussian method

I remind you that Gaussian method does not imply unambiguous rigidity, and your decision will most likely differ from my decision. A brief example of a task at the end of the lesson.

Which method should I use to find the rank of a matrix?

In practice, it is often not stated at all which method should be used to find the rank. In such a situation, the condition should be analyzed - for some matrices it is more rational to solve through minors, while for others it is much more profitable to apply elementary transformations:

Example 5

Find the rank of a matrix

Solution: the first method somehow immediately disappears =)

A little higher, I advised not to touch the columns of the matrix, but when there is a zero column, or proportional/coinciding columns, then it is still worth amputating:

(1) The fifth column is zero, remove it from the matrix. Thus, the rank of the matrix is ​​no more than four. The first line was multiplied by –1. This is another signature feature of the Gauss method, which turns the following action into a pleasant walk:

(2) To all lines, starting from the second, the first line was added.

(3) The first line was multiplied by –1, the third line was divided by 2, the fourth line was divided by 3. The second line was added to the fifth line, multiplied by –1.

(4) The third line was added to the fifth line, multiplied by –2.

(5) The last two lines are proportional, the fifth is deleted.

The result is 4 lines.

Answer:

Standard five-story building for independent study:

Example 6

Find the rank of a matrix

A short solution and answer at the end of the lesson.

It should be noted that the phrase “matrix rank” is not so often seen in practice, and in most problems you can do without it altogether. But there is one task where the concept in question is the main character, and we will conclude the article with this practical application:

How to study a system of linear equations for consistency?

Often, in addition to the solution systems of linear equations according to the condition, it is first required to examine it for compatibility, that is, to prove that any solution exists at all. A key role in such verification is played by Kronecker-Capelli theorem, which I will formulate in the necessary form:

If rank system matrices equal to rank extended matrix system, then the system is consistent, and if this number coincides with the number of unknowns, then the solution is unique.

Thus, to study the system for compatibility it is necessary to check the equality , Where - system matrix(remember the terminology from the lesson Gauss method), A - extended system matrix(i.e. a matrix with coefficients of variables + a column of free terms).

To work with the concept of matrix rank, we will need information from the topic "Algebraic complements and minors. Types of minors and algebraic complements." First of all, this concerns the term “matrix minor”, ​​since we will determine the rank of the matrix precisely through the minors.

Matrix rank is the maximum order of its minors, among which there is at least one that is not equal to zero.

Equivalent matrices- matrices whose ranks are equal to each other.

Let us explain in more detail. Suppose that among the second-order minors there is at least one that is different from zero. And all minors whose order is higher than two are equal to zero. Conclusion: the rank of the matrix is ​​2. Or, for example, among the minors of the tenth order there is at least one that is not equal to zero. And all minors whose order is higher than 10 are equal to zero. Conclusion: the rank of the matrix is ​​10.

The rank of the matrix $A$ is denoted as follows: $\rang A$ or $r(A)$. The rank of the zero matrix $O$ is assumed to be zero, $\rang O=0$. Let me remind you that to form a matrix minor you need to cross out rows and columns, but it is impossible to cross out more rows and columns than the matrix itself contains. For example, if the matrix $F$ has size $5\times 4$ (i.e. contains 5 rows and 4 columns), then the maximum order of its minors is four. It will no longer be possible to form minors of the fifth order, since they will require 5 columns (and we have only 4). This means that the rank of the matrix $F$ cannot be more than four, i.e. $\rang F≤4$.

In more general form, the above means that if a matrix contains $m$ rows and $n$ columns, then its rank cannot exceed the smallest of $m$ and $n$, i.e. $\rang A≤\min(m,n)$.

In principle, from the very definition of rank follows the method for finding it. The process of finding the rank of a matrix, by definition, can be schematically represented as follows:

Let me explain this diagram in more detail. Let's start reasoning from the very beginning, i.e. from the first order minors of some matrix $A$.

1. If all first-order minors (i.e., elements of the matrix $A$) are equal to zero, then $\rang A=0$. If among the first-order minors there is at least one that is not equal to zero, then $\rang A≥ 1$. Let's move on to checking second-order minors.
2. If all second-order minors are equal to zero, then $\rang A=1$. If among the second-order minors there is at least one that is not equal to zero, then $\rang A≥ 2$. Let's move on to checking third-order minors.
3. If all third-order minors are equal to zero, then $\rang A=2$. If among the third-order minors there is at least one that is not equal to zero, then $\rang A≥ 3$. Let's move on to checking fourth-order minors.
4. If all fourth-order minors are equal to zero, then $\rang A=3$. If among the fourth-order minors there is at least one that is not equal to zero, then $\rang A≥ 4$. We move on to checking fifth-order minors and so on.

What awaits us at the end of this procedure? It is possible that among the kth order minors there will be at least one that is different from zero, and all (k+1) order minors will be equal to zero. This means that k is the maximum order of minors, among which there is at least one that is not equal to zero, i.e. the rank will be equal to k. There may be a different situation: among the kth order minors there will be at least one that is not equal to zero, but it will no longer be possible to form (k+1) order minors. In this case, the rank of the matrix is ​​also equal to k. In short, the order of the last composed non-zero minor will be equal to the rank of the matrix.

Let's move on to examples in which the process of finding the rank of a matrix, by definition, will be clearly illustrated. Let me emphasize once again that in the examples of this topic we will begin to find the rank of matrices using only the definition of rank. Other methods (calculating the rank of a matrix using the method of bordering minors, calculating the rank of a matrix using the method of elementary transformations) are discussed in the following topics.

By the way, it is not at all necessary to start the procedure for finding the rank with minors of the smallest order, as was done in examples No. 1 and No. 2. You can immediately move on to minors of higher orders (see example No. 3).

Example No. 1

Find the rank of the matrix $A=\left(\begin(array)(ccccc) 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end(array) \right)$.

This matrix has size $3\times 5$, i.e. contains three rows and five columns. Of the numbers 3 and 5, the minimum is 3, therefore the rank of the matrix $A$ is no more than 3, i.e. $\rang A≤ 3$. And this inequality is obvious, since we will no longer be able to form fourth-order minors - they require 4 rows, and we have only 3. Let’s move on directly to the process of finding the rank of a given matrix.

Among the first order minors (i.e. among the elements of the matrix $A$) there are non-zero ones. For example, 5, -3, 2, 7. In general, we are not interested in the total number of non-zero elements. There is at least one non-zero element - and that's enough. Since among the first-order minors there is at least one non-zero, we conclude that $\rang A≥ 1$ and proceed to checking the second-order minors.

Let's start exploring second order minors. For example, at the intersection of rows No. 1, No. 2 and columns No. 1, No. 4 there are elements of the following minor: $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right| $. For this determinant, all elements of the second column are equal to zero, therefore the determinant itself is equal to zero, i.e. $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=0$ (see property No. 3 in the topic of properties of determinants). Or you can simply calculate this determinant using formula No. 1 from the section on calculating second- and third-order determinants:

$$ \left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=5\cdot 0-0\cdot 7=0. $$

The first second-order minor we tested turned out to be equal to zero. What does this mean? About the need to further check second-order minors. Either they will all turn out to be zero (and then the rank will be equal to 1), or among them there will be at least one minor that is different from zero. Let's try to make a better choice by writing a second-order minor, the elements of which are located at the intersection of rows No. 1, No. 2 and columns No. 1 and No. 5: $\left|\begin(array)(cc) 5 & 2 \\ 7 & 3 \end(array) \right|$. Let's find the value of this second-order minor:

$$ \left|\begin(array)(cc) 5 & 2 \\ 7 & 3 \end(array) \right|=5\cdot 3-2\cdot 7=1. $$

This minor is not equal to zero. Conclusion: among the second-order minors there is at least one non-zero. Therefore $\rang A≥ 2$. We need to move on to studying third-order minors.

If we choose column No. 2 or column No. 4 to form third-order minors, then such minors will be equal to zero (since they will contain a zero column). It remains to check only one third-order minor, the elements of which are located at the intersection of columns No. 1, No. 3, No. 5 and rows No. 1, No. 2, No. 3. Let's write down this minor and find its value:

$$ \left|\begin(array)(ccc) 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end(array) \right|=-20-18-14 +16+21+15=0. $$

So, all third order minors are equal to zero. The last non-zero minor we compiled was of second order. Conclusion: the maximum order of minors, among which there is at least one non-zero, is 2. Therefore, $\rang A=2$.

Answer: $\rang A=2$.

Example No. 2

Find the rank of the matrix $A=\left(\begin(array) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end(array) \right)$.

We have a square matrix of the fourth order. Let us immediately note that the rank of this matrix does not exceed 4, i.e. $\rang A≤ 4$. Let's start finding the rank of the matrix.

Among the first-order minors (i.e., among the elements of the matrix $A$) there is at least one that is not equal to zero, therefore $\rang A≥ 1$. Let's move on to checking second-order minors. For example, at the intersection of rows No. 2, No. 3 and columns No. 1 and No. 2, we obtain the following second-order minor: $\left| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|$. Let's calculate it:

$$\left| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|=0-10=-10. $$

Among the second-order minors there is at least one that is not equal to zero, so $\rang A≥ 2$.

Let's move on to third-order minors. Let's find, for example, a minor whose elements are located at the intersection of rows No. 1, No. 3, No. 4 and columns No. 1, No. 2, No. 4:

$$\left | \begin(array) (cccc) -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end(array) \right|=105-105=0. $$

Since this third-order minor turned out to be equal to zero, it is necessary to investigate another third-order minor. Either all of them will be equal to zero (then the rank will be equal to 2), or among them there will be at least one that is not equal to zero (then we will begin to study fourth-order minors). Let's consider a third-order minor, the elements of which are located at the intersection of rows No. 2, No. 3, No. 4 and columns No. 2, No. 3, No. 4:

$$\left| \begin(array) (ccc) -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end(array) \right|=-28. $$

Among the third-order minors there is at least one non-zero, so $\rang A≥ 3$. Let's move on to checking fourth-order minors.

Any fourth-order minor is located at the intersection of four rows and four columns of the matrix $A$. In other words, the fourth-order minor is the determinant of the matrix $A$, since this matrix contains 4 rows and 4 columns. The determinant of this matrix was calculated in example No. 2 of the topic “Reducing the order of the determinant. Decomposing the determinant in a row (column)”, so let’s just take the finished result:

$$\left| \begin(array) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end (array)\right|=86. $$

So the fourth order minor is not equal to zero. We can no longer form minors of the fifth order. Conclusion: the highest order of minors, among which there is at least one non-zero, is 4. Result: $\rang A=4$.

Answer: $\rang A=4$.

Example No. 3

Find the rank of the matrix $A=\left(\begin(array) (cccc) -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end( array) \right)$.

Let us immediately note that this matrix contains 3 rows and 4 columns, so $\rang A≤ 3$. In the previous examples, we began the process of finding the rank by considering minors of the smallest (first) order. Here we will try to immediately check the minors of the highest possible order. For the matrix $A$ these are the third order minors. Let's consider a third-order minor, the elements of which lie at the intersection of rows No. 1, No. 2, No. 3 and columns No. 2, No. 3, No. 4:

$$\left| \begin(array) (ccc) 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end(array) \right|=-8-60-20=-88. $$

So, the highest order of minors, among which there is at least one that is not equal to zero, is 3. Therefore, the rank of the matrix is ​​3, i.e. $\rang A=3$.

Answer: $\rang A=3$.

In general, finding the rank of a matrix by definition is, in the general case, a rather labor-intensive task. For example, a relatively small matrix of size $5\times 4$ has 60 second-order minors. And even if 59 of them are equal to zero, then the 60th minor may turn out to be non-zero. Then you will have to study third-order minors, of which this matrix has 40 pieces. Usually they try to use less cumbersome methods, such as the method of bordering minors or the method of equivalent transformations.

“If you want to learn to swim, then boldly enter the water, and if you want to learn to solve problems, That solve them.»
D. Polya (1887-1985)

(Mathematician. Made a great contribution to the popularization of mathematics. Wrote several books about how to solve problems and how to teach solving problems.)

Consider the matrix

Let's highlight in it k-rows And k-columns (k≤(min(m,n))). From the elements located at the intersection of the selected rows and columns, we will compose a determinant kth order. All such determinants are called minors of this matrix.

Let's consider all possible matrix minors A, different from zero.

Matrix rank A is the largest order of the non-zero minor of this matrix.

If all elements of a matrix are equal to zero, then the rank of this matrix is ​​assumed to be zero.

A minor whose order determines the rank of the matrix is ​​called basic.

A matrix can have several basis minors.

Matrix rank A denoted by r(A). If r(A)=r(B), then the matrices A And IN are called equivalent. They write A̴∼B.

Matrix rank properties:

1. When a matrix is ​​transposed, its rank does not change.
2. If you delete the zero row (column) from the matrix, the rank of the matrix will not change.
3. The rank of the matrix does not change during elementary matrix transformations.

By elementary transformations we mean:

• Rearranging matrix rows;
• Multiplying a string by a number other than zero;
• Adding to the elements of one line the corresponding elements of another line, multiplied by an arbitrary number.

When calculating the rank of a matrix, elementary transformations, the method of reducing the matrix to a stepwise form, and the method of bordering minors can be used.

Method for reducing a matrix to a stepwise The idea is that with the help of elementary transformations this matrix is ​​reduced to a step matrix.

The matrix is ​​called stepped , if in each of its lines the first non-zero element is to the right than in the previous one (i.e., steps are obtained, the height of each step must be equal to one).

Examples of step matrices:

Examples of non-echelon matrices:

EXAMPLE: Find the rank of the matrix:

SOLUTION:

Let us reduce this matrix to a step matrix using elementary transformations.

1. Swap the first and third lines.

2. We get zeros under one in the first column.

By adding the first line multiplied by (-3) to the second line, the first line multiplied by (-5) to the third line, and the first line multiplied by (-3) to the fourth line, we get

To make it clearer where else you need to get zeros, let’s draw steps in the matrix. (The matrix will be stepped if there are zeros everywhere under the steps)

3. By adding the second line multiplied by (-1) to the third line, and the second line multiplied by (-1) to the fourth line, we get zeros under the steps in the second column.

If we draw the steps again, we will see that the matrix is ​​stepped.

Her rank is r=3(the number of rows of the step matrix, in each of which at least one element is different from zero). Therefore, the rank of this matrix r=3.

The solution can be written like this:

(Roman numerals indicate line numbers)

Answer: r=3.

Minor order k+1, containing a minor of order k called bordering the minor.

Method of bordering minors is based on the fact that the rank of a given matrix is ​​equal to the order of a minor of this matrix that is non-zero, and all minors bordering it are equal to zero.